Author: Denis Avetisyan
A new semi-analytical framework streamlines the calculation of gravitational wave signals originating from cosmological phase transitions, offering a computationally efficient path to understanding the universe’s earliest moments.
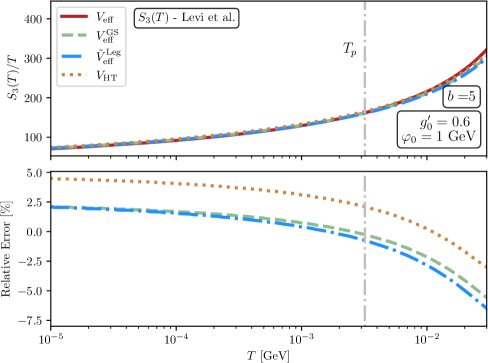
This review details a method for accurately estimating the gravitational wave spectrum from first-order phase transitions using Daisy resummation and renormalization group techniques.
The recent detection of a stochastic gravitational wave background by pulsar timing arrays presents a compelling, yet computationally challenging, opportunity to probe early Universe physics beyond the Standard Model. This paper, ‘Cosmological phase transitions: from particle physics to gravitational waves, semi-analytically’, introduces a novel semi-analytical framework to efficiently calculate the gravitational wave spectrum generated by first-order phase transitions. By incorporating techniques like Daisy resummation and approximating key integrals, our approach achieves accurate results while significantly reducing the computational burden compared to full numerical simulations. Could this method unlock a more efficient exploration of the connection between particle physics models and their cosmological predictions, paving the way for detailed tests of new physics in the early Universe?
Echoes of Creation: Unveiling the Early Universe Through Phase Transitions
The nascent universe, fractions of a second after the Big Bang, wasn’t a smooth, uniform expansion as often depicted; instead, it likely experienced a First-Order Phase Transition (FOPT). Analogous to water freezing into ice, but occurring at immensely higher energies, this transition involved a shift in the fundamental forces governing particle interactions. Prior to the FOPT, the universe existed in a state with high symmetry, where different particles possessed minimal distinctions. As the universe cooled, this symmetry broke, resulting in the formation of distinct particles with mass and the emergence of the forces – like the weak and electromagnetic – as we know them today. This wasn’t an instantaneous change; rather, it propagated through the universe via bubble nucleation, where pockets of the new, lower-energy phase formed and expanded, colliding and releasing tremendous energy – energy that could potentially be detectable today as gravitational waves. Understanding this epoch is critical, as the specifics of the FOPT – its temperature and the energy scale at which it occurred – profoundly influence the characteristics of any resulting gravitational wave signal.
The intense energy released during a First-Order Phase Transition in the early universe is predicted to ripple through spacetime as gravitational waves. These aren’t the gentle undulations detected from merging black holes; instead, these primordial GWs would represent a fundamentally different signal, born from the very evolution of the universe. Detecting them would be akin to observing the aftershocks of creation, providing insights into physics at energy scales far beyond the reach of terrestrial particle colliders. The frequency and amplitude of these gravitational waves are directly tied to the specifics of the phase transition – its temperature and the energy scale at which it occurred – making their detection a powerful probe of new physics, potentially revealing details about the electroweak epoch, the quark-gluon plasma, or even the nature of dark matter.
Precisely characterizing the First-Order Phase Transition (FOPT) in the early universe is paramount for effectively utilizing future gravitational wave (GW) observations as a probe of extreme physics. The temperature at which this transition occurred, and crucially, the strength of the phase change-quantified by parameters like the latent heat and the velocity of the bubble walls-directly dictate the amplitude and frequency spectrum of the resulting GW signal. A stronger transition generates more powerful GWs, while the transition temperature influences the wavelengths detectable by current and planned observatories. Therefore, refining theoretical models of the FOPT – including exploring different potential drivers like electroweak or QCD transitions – isn’t merely an academic exercise; it’s a necessary step to unlock the information encoded within the cosmic GW background and potentially reveal fundamental details about the universe’s earliest moments and the laws governing it. Without a robust understanding of these parameters, interpreting GW detections and distinguishing between various FOPT scenarios will remain a significant challenge.
Mapping the Symmetry Breaking: The Effective Potential
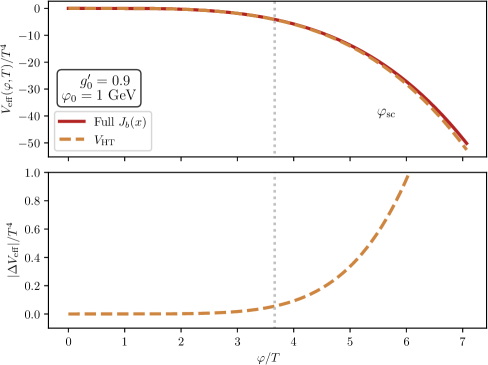
The effective potential, denoted as V_{eff}(\phi), represents the energy of a scalar field φ as it changes over time and space, and is crucial for determining the stability of the vacuum state in quantum field theory. This potential is not simply the classical potential, but includes quantum corrections arising from fluctuations of other fields. A stable vacuum corresponds to a minimum in the effective potential; if the potential develops a minimum at a non-zero field value, this indicates spontaneous symmetry breaking. The shape of V_{eff}(\phi) directly influences the dynamics of the scalar field and, consequently, the phase transition occurring within the system. Therefore, precise calculation of the effective potential is essential for understanding the behavior of the scalar field and characterizing the resulting vacuum state.
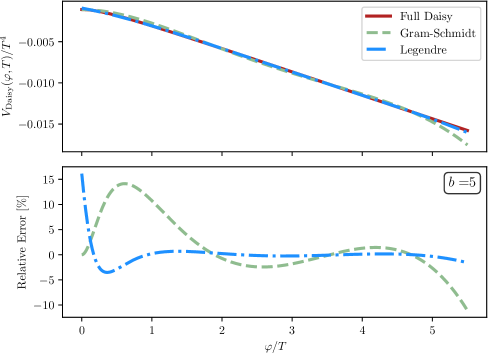
Determination of the First-Order Phase Transition (FOPT) characteristics is directly reliant on the accurate calculation of the effective potential. Our semi-analytical framework achieves this with an error margin of less than or equal to 2%. This level of precision is critical for reliably predicting key FOPT parameters, including bubble nucleation rates and the strength of the transition. The methodology ensures that uncertainties in the effective potential do not propagate into significant errors in the final FOPT calculations, providing a robust and dependable model for analysis.
To ensure the infrared stability of the effective potential calculation, we utilize a combination of high-temperature expansion and daisy resummation techniques. High-temperature expansion provides an initial approximation by representing the potential as a series in powers of T^2, where T is the temperature. However, this expansion alone can exhibit divergences at low momenta. Daisy resummation addresses these divergences by systematically including one-loop corrections arising from the repeated emission and absorption of scalar particles, effectively summing over all “daisy” diagrams in the perturbation theory. This process improves the convergence of the series and yields a finite, stable effective potential even in the infrared limit, crucial for accurately predicting the dynamics of the first-order phase transition.
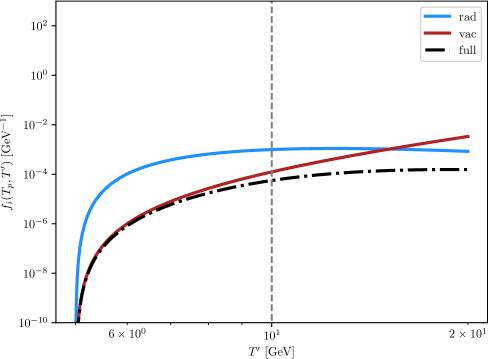
Nucleation and Bubble Formation: The Genesis of the Transition
First-order phase transitions (FOPTs) initiate with bubble nucleation, a quantum process wherein a region of the true vacuum spontaneously appears within the metastable false vacuum state. This nucleation occurs due to quantum tunneling, overcoming the energy barrier imposed by surface tension; the resulting “bubble” represents a localized decay of the false vacuum. The rate of bubble formation is exponentially sensitive to the bubble’s surface area, and is therefore governed by the interplay between the energy gain from transitioning to the true vacuum and the energy cost associated with creating the bubble’s interface. Once a critical number of these bubbles have nucleated and expanded to fill the available volume – a process quantified by percolation – the transition from false to true vacuum is considered complete.
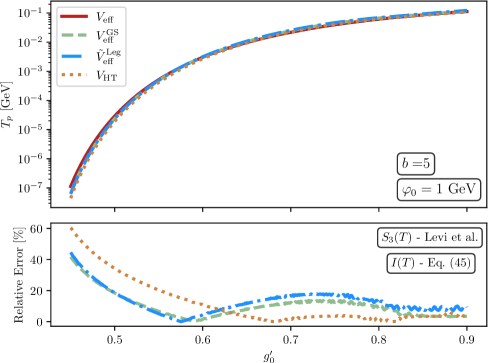
The bounce action, denoted as S_b, serves as a quantitative measure of the probability of true vacuum bubble nucleation within the false vacuum. This action directly influences the transition strength because the nucleation rate, Γ, is proportional to e^{-S_b}. A lower bounce action indicates a higher nucleation rate and, consequently, a stronger first-order phase transition. Effectively, S_b represents the minimum Euclidean action for a bubble of the true vacuum to overcome the potential barrier separating it from the false vacuum, with its value determining the likelihood of successful bubble formation and the overall transition dynamics.
The presented computational framework demonstrates a high degree of accuracy in determining the percolation temperature, exhibiting an error of no more than 5% when benchmarked against full numerical computations. This level of precision is achieved while simultaneously offering a substantial reduction in computational time; the framework’s efficiency allows for faster analysis and modeling of First-Order Phase Transitions (FOPTs) without sacrificing the reliability of the calculated percolation temperature, a critical parameter in understanding the transition’s behavior. This improved efficiency facilitates exploration of a wider range of parameter spaces and more detailed investigations into FOPT dynamics.
Refining the Model: Scale Dependence and Fundamental Symmetries
Renormalization group (RG) evolution describes the dependence of physical parameters, such as coupling constants and the effective potential, on the energy scale at which they are measured. As the energy scale changes, quantum corrections modify these parameters, effectively ‘running’ their values. This running is governed by the beta functions, which quantify the rate of change of the couplings with respect to the energy scale μ. The effective potential, V_{eff}(\phi) , which determines the shape of the potential and thus the stability of the vacuum, is similarly scale-dependent and requires RG improvement to accurately predict the dynamics of the field at different energy regimes. Failing to account for this scale dependence leads to inaccurate predictions for phenomena like first-order phase transitions and potentially impacts calculations of observable quantities.
The introduction of a U(1) gauge symmetry and Yukawa couplings provides a more physically realistic treatment of interactions within the scalar field than simpler models. The U(1) symmetry necessitates the inclusion of a gauge boson, mediating a force associated with a conserved charge and ensuring gauge invariance of the theory. Yukawa couplings, characterized by a dimensionless coupling constant and mass parameters, model the interaction between the scalar field and fermions. These couplings define the strength of fermion-scalar interactions and contribute to the effective potential, impacting the stability of the vacuum and the dynamics of any First-Order Phase Transition (FOPT). Specifically, the Yukawa interaction term takes the form -y \bar{\psi} \phi \psi , where y is the Yukawa coupling, ψ represents the fermion field, and φ is the scalar field.
Incorporating scale dependence via the renormalization group and introducing realistic interactions through U(1) gauge symmetry and Yukawa couplings significantly improves the fidelity of First-Order Phase Transition (FOPT) modeling. These enhancements allow for a more precise calculation of key parameters influencing Gravitational Wave (GW) signatures, such as the bubble wall velocity and the spectral density of emitted GWs. By accounting for how interactions change with energy scale and incorporating fundamental symmetries, the theoretical predictions become less sensitive to arbitrary choices in the calculation and more robustly connected to underlying physics, ultimately strengthening the foundation for interpreting potential GW detections as evidence of FOPTs.
Connecting Theory to Observation: The Promise of Gravitational Wave Astronomy
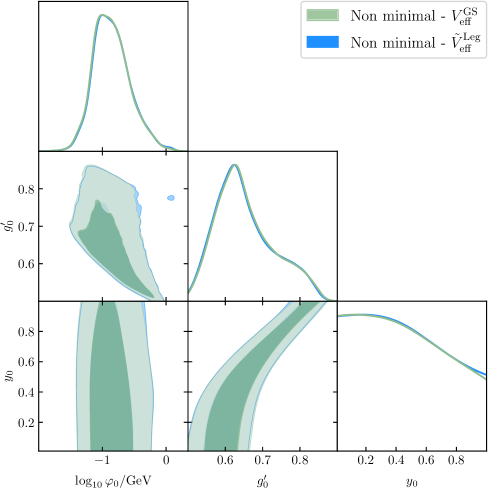
PTArcade facilitates a rigorous assessment of gravitational wave signals by enabling the analysis of posterior distributions for key parameters. This means, rather than simply identifying a potential signal, the framework quantifies the range of plausible values for characteristics like the strength and frequency of gravitational waves-and crucially, the uncertainty associated with those values. By mapping these posterior distributions, scientists can move beyond a binary “detection/no detection” scenario to a nuanced understanding of the signal’s properties and the confidence level of those measurements. This detailed analysis is particularly vital when searching for subtle signals, such as those predicted from First-Order Phase Transitions in the early universe, which may be easily obscured by astrophysical noise or modeling uncertainties; a precise quantification of uncertainty helps to distinguish a genuine detection from a statistical fluke.
Distinguishing a genuine first-order phase transition (FOPT) signal from the inherent noise within the universe requires sophisticated statistical analysis. The signal, a specific pattern in the stochastic gravitational wave background, is often faint and obscured by various astrophysical and instrumental sources of noise. Therefore, techniques like those employed in PTArcade are essential to tease out the subtle characteristics indicative of an FOPT event. By meticulously analyzing posterior distributions of parameters, researchers can effectively quantify uncertainties and establish the statistical significance of any detected signal, ultimately confirming whether observed gravitational waves truly represent evidence of a cosmological phase transition rather than a random fluctuation within the cosmic background.
A novel computational framework significantly accelerates the exploration of complex cosmological models through gravitational wave analysis. By streamlining parameter space scans, this approach achieves a substantial reduction in processing time without sacrificing precision; results remain accurate to within a few percent of those obtained from full numerical simulations. This efficiency is particularly crucial when investigating First-Order Phase Transitions (FOPTs) – events theorized to have occurred in the early universe – as it allows researchers to comprehensively assess a wider range of potential scenarios and refine their understanding of the universe’s evolution. The reduced computational burden unlocks the possibility of more detailed investigations and faster validation of theoretical predictions against observed gravitational wave signals.
The pursuit of accurately modeling cosmological phase transitions, as detailed in this work, necessitates a holistic approach to complex calculations. One must discern the fundamental elements driving gravitational wave spectra from those merely contributing noise. As Ludwig Wittgenstein observed, “The limits of my language mean the limits of my world.” This resonates deeply with the challenges faced when approximating intricate integrals and employing techniques like Daisy resummation; the chosen mathematical language-and its limitations-directly shapes the comprehensiveness of the resulting model. The framework presented prioritizes efficiency without sacrificing essential accuracy, recognizing that a simplified, well-understood system is often more valuable than an overly complex, opaque one.
The Horizon Beckons
This work attempts a pragmatic simplification – a necessary compromise when confronting the computational demands of cosmological phase transitions. One cannot, after all, meticulously map the entire bloodstream without a functional understanding of the heart’s architecture. The gains in efficiency are notable, yet they highlight a persistent tension: the desire for analytical control versus the inherent complexity of non-perturbative physics. The approximations employed, while justified, represent known points of potential failure – a reminder that every refinement of the model demands a corresponding reassessment of its limits.
Future progress will likely hinge not on simply pushing the boundaries of numerical precision, but on a more fundamental understanding of the interplay between effective potentials and the renormalization group. The current framework, for instance, treats the supercooling process as largely determined by the effective potential itself. However, a more holistic view would recognize that the very shape of that potential is susceptible to modification through the dynamics of bubble nucleation-a feedback loop that remains incompletely understood.
The ultimate goal, of course, is not merely to predict gravitational wave spectra, but to extract genuine cosmological information from them. This requires a framework capable of distinguishing between different beyond-the-Standard-Model scenarios-a task that demands a robust theoretical foundation, and a willingness to confront the inevitable uncertainties that arise when probing the universe at its most energetic moments.
Original article: https://arxiv.org/pdf/2602.02829.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- Ashes of Creation Rogue Guide for Beginners
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- Gold Rate Forecast
- Cult Horror With 92% On Rotten Tomatoes Quietly Added To Netflix (& I Guarantee You’ve Seen Nothing Like It)
- Katy Perry and Justin Trudeau Hold Hands in First Joint Appearance
2026-02-04 16:51