Author: Denis Avetisyan
A new analysis of the quantum XY chain reveals how complex partition functions and Fisher zeros map out its exotic phase behavior and spectral properties.
This review details the application of complex partition functions and Fisher zeros to characterize quantum criticality and spectral weight in the one-dimensional XY model.
Understanding the intricate interplay between quantum fluctuations and emergent phases remains a central challenge in condensed matter physics. In the article ‘Giant bubbles of Fisher zeros in the quantum XY chain’, we introduce a novel approach leveraging complex-valued partition functions and thermofield dynamics to characterize the quantum properties of this paradigmatic one-dimensional model. Our analysis reveals the presence of large-scale ‘bubbles’ of Fisher zeros-singularities in the partition function-which define a characteristic energy scale seemingly at odds with predictions for the expected Luttinger liquid behavior. Do these Fisher-zero bubbles offer a new lens through which to explore pseudogap formation and spectral weight transfer in strongly correlated systems?
The One-Dimensional XY Model: A Playground for Quantum Complexity
The study of many-body quantum systems – those comprising numerous interacting particles – routinely confronts researchers with intractable mathematical challenges. Conventional analytical methods, such as perturbation theory, often falter when dealing with strong interactions or complex correlations between particles. This limitation arises because the exponential growth of the Hilbert space – the mathematical space encompassing all possible states of the system – quickly overwhelms computational resources and analytical techniques. Consequently, gaining a comprehensive understanding of emergent phenomena – the collective behaviors arising from these interactions – remains a significant hurdle. These systems, however, are crucial for describing a vast range of physical phenomena, from superconductivity and magnetism to the behavior of materials at extreme conditions, necessitating the development of novel theoretical and computational approaches to circumvent these longstanding difficulties.
The seemingly simple one-dimensional XY model, a cornerstone of theoretical physics, belies a surprisingly complex tapestry of quantum behavior. This model, describing interacting spins along a line, doesn’t merely offer a simplified scenario; it serves as a crucial proving ground for understanding more intricate many-body quantum systems. Investigations reveal that the XY model exhibits distinct quantum phases, transitioning between ferromagnetic and antiferromagnetic order as external parameters are adjusted – a phenomenon known as a quantum phase transition. Furthermore, the model showcases strong quantum correlations, where the state of one spin is inextricably linked to others, even across significant distances. This combination of phase transitions and correlations makes the 1D XY model an invaluable testbed for developing and validating new theoretical techniques aimed at unraveling the mysteries of quantum matter, offering insights applicable to a broad range of physical systems.
Characterizing the 1D XY model demands analytical approaches that surpass the limitations of traditional perturbation theory, a method effective only for weakly interacting systems. The model’s intricate energy landscape, arising from strong quantum correlations, necessitates techniques capable of mapping and interpreting its non-perturbative features. Researchers employ methods like bosonization and exact diagonalization to access the system’s ground state and excited states, revealing the presence of collective modes and quantum phase transitions. These investigations aren’t merely about solving an equation; they’re about visualizing a complex, multi-dimensional surface where the system seeks its lowest energy configuration, a process that defines its macroscopic behavior and highlights the emergence of quantum phenomena beyond simple, isolated particle interactions. The challenge lies in effectively navigating this landscape to understand how interactions give rise to the system’s unique properties.
Extending the Partition Function: Probing Beyond Equilibrium
The traditional partition function, Z = \sum_{s} e^{-\beta H_s}, is defined for real inverse temperatures β. The complex partition function extends this definition to complex values of β, enabling analytical continuation beyond the range of convergence for real β. This continuation allows for the investigation of systems in regimes not accessible through conventional statistical mechanics, such as exploring behavior at imaginary temperatures or accessing dynamical properties. By extending the partition function into the complex plane, researchers can extract information about non-equilibrium states and time-dependent phenomena, circumventing limitations imposed by the requirement of thermal equilibrium in standard methods. This technique provides a powerful tool for analyzing systems driven far from equilibrium or exhibiting transient behavior.
The utilization of complex parameters, specifically a complex inverse temperature β, within the partition function allows for the investigation of systems driven out of thermal equilibrium. Standard statistical mechanics relies on real values of β, restricting analysis to equilibrium states. Extending β into the complex plane enables analytical continuation of the partition function beyond its radius of convergence, accessing regimes corresponding to non-equilibrium dynamics and responses. This technique effectively introduces a ‘time-like’ component to the thermal parameter, allowing the exploration of transient behaviors and the characterization of systems that are not in a steady state, thereby providing insights into relaxation processes and response functions unavailable through traditional methods.
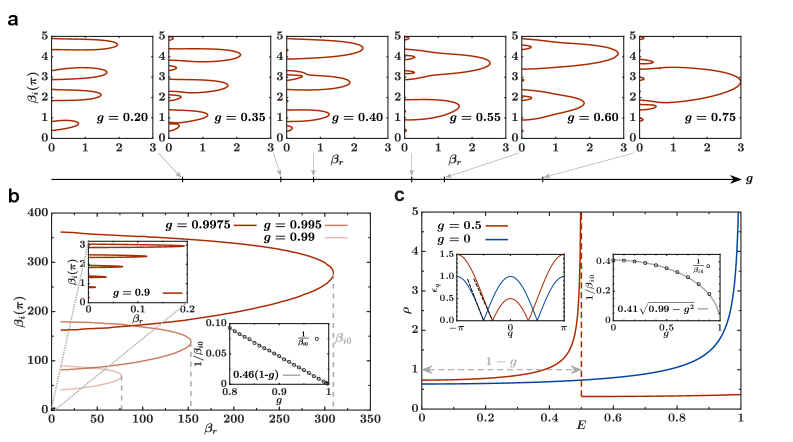
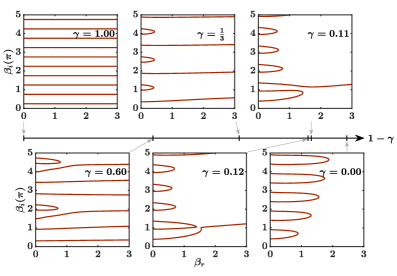
The identification of Fisher zeros – the zeros of the complex partition function in the complex inverse temperature plane – provides a method for determining phase transitions and critical points within a quantum system. These zeros are not randomly distributed; their locations reveal information about the system’s stability and critical behavior. Specifically, this work demonstrates the existence of large, coalescing regions – termed ‘giant bubbles’ – of Fisher zeros as the system approaches the XX limit, a highly symmetric point in parameter space. The density and arrangement of these zeros within the complex plane directly correlate with the system’s susceptibility and the nature of the phase transition, offering a complementary approach to traditional critical exponents and order parameters. Analyzing the location of these β zeros allows for the determination of critical temperatures and the characterization of the associated singularities.
Spectral Signatures of Quantum Behavior: From Weight to Pseudogaps
The spectral weight distribution quantifies the oscillator strength – a measure of the probability of transitions between quantum states – as a function of energy. This distribution directly reflects the system’s excitation spectrum, revealing which energy levels are most readily accessed by external perturbations. Specifically, the area under the spectral weight curve at a given energy corresponds to the total probability of exciting the system to states at or above that energy. Analyzing the shape and distribution of spectral weight provides insights into the electronic structure and many-body interactions within a material, as changes in the distribution indicate modifications to the allowed excitations and their relative strengths. \sum_{\omega} A(\omega) = 1 , where A(\omega) represents the spectral weight at energy ω, demonstrates the normalization condition reflecting total oscillator strength.
In the one-dimensional XY model, a pseudogap manifests as a noticeable reduction in spectral weight at lower energy levels. This suppression is not due to a true gap in the single-particle excitation spectrum, but rather arises from strong correlations between particles within the system. These correlations effectively redistribute the spectral weight, leading to a depletion of low-energy excitations and the formation of the pseudogap feature. The size of the pseudogap is directly related to the strength of these interactions, serving as an indicator of the degree of collective behavior present in the system. The observation of a pseudogap, therefore, confirms that the XY model exhibits many-body effects beyond simple independent particle behavior.
The presence of a pseudogap in the excitation spectrum is directly related to the Van Hove singularity within the system’s density of states D(\omega) . Van Hove singularities represent points in the energy spectrum where the density of states diverges, arising from specific band structure features. In strongly correlated systems, interactions between electrons modify the single-particle band structure and, consequently, the position and intensity of these singularities. The pseudogap manifests as a suppression of spectral weight near the Van Hove singularity, indicating that many-body effects effectively reduce the available single-particle excitations at low energies, and thus alter the expected density of states profile.
Thermalization and Beyond: Implications for Complex Systems
The Eigenstate Thermalization Hypothesis (ETH) challenges conventional understanding of quantum systems by suggesting that even isolated ones – those with no external interaction – will eventually equilibrate, behaving as if they were in thermal equilibrium with a much larger ensemble. This isn’t a simple approach to equilibrium, however; the ETH posits this happens through the properties of individual energy eigenstates. Specifically, these eigenstates are expected to encode statistical information, meaning that physical observables calculated from them will statistically resemble the predictions of a standard thermal ensemble, like the microcanonical or canonical ensemble. This implies that detailed information about the initial conditions is effectively ‘lost’ as the system evolves, with long-time averages determined solely by the system’s conserved quantities. The remarkable implication is that quantum chaos-the unpredictable behavior of quantum systems-can give rise to statistically predictable thermal behavior, bridging the gap between quantum mechanics and statistical mechanics, and offering a potential explanation for the emergence of classicality from the quantum realm.
Rigorous testing of the Eigenstate Thermalization Hypothesis (ETH) necessitates delving into the system’s spectral properties, and the complex partition function alongside the spectral form factor provide powerful analytical tools for this purpose. These mathematical constructs effectively map the distribution of energy levels and their associated fluctuations, revealing whether a quantum system truly equilibrates as predicted by the ETH. Recent investigations utilizing these tools have focused on the 1D XY model – a fundamental model in condensed matter physics exhibiting quantum phase transitions – and have yielded compelling evidence supporting the hypothesis. Specifically, analysis demonstrates that the spectral form factor aligns with theoretical predictions based on random matrix theory, indicating that energy levels are sufficiently scrambled to establish thermal equilibrium even in an isolated system, solidifying the understanding of how complex quantum systems approach stability.
Investigations leveraging the ‘Boundary Partition Function’ represent a powerful extension of thermalization frameworks, allowing researchers to probe dynamical quantum phase transitions – shifts in a system’s properties driven by time-dependent parameters rather than temperature. This approach diverges from traditional equilibrium studies by focusing on the system’s response to external drives, revealing non-equilibrium phases characterized by distinct order parameters and critical behaviors. By examining how the boundary partition function evolves under these drives, scientists can map out the phase diagram in the time domain, identifying critical points where the system undergoes abrupt transitions between different dynamical phases. This methodology is particularly valuable for understanding systems far from equilibrium, such as those found in quenched materials or driven by external fields, offering insights into the fundamental mechanisms governing non-equilibrium dynamics and the emergence of complex behavior.
Revealing Hidden Order: Oscillatory Phases and Finite-Size Gaps
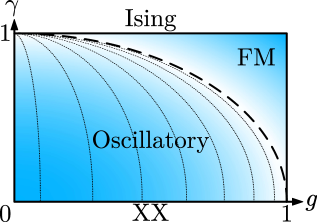
The one-dimensional XY model presents a fascinating oscillatory phase, diverging from typical condensed matter systems through its peculiar behavior at finite size. This phase is defined by oscillating Δ gaps – energy differences separating ground and excited states – that fluctuate with system size. These oscillations aren’t merely numerical quirks; they are deeply connected to the model’s underlying physics and the emergence of unusual Fisher zero configurations. These configurations represent special arrangements of spins where the energy approaches zero, contributing to the system’s unique critical properties and distinct from the behavior observed in simpler spin models. The interplay between these oscillating gaps and Fisher zeros gives rise to a rich and complex phase diagram, marking the XY model as a compelling platform for exploring novel quantum phenomena in reduced dimensions.
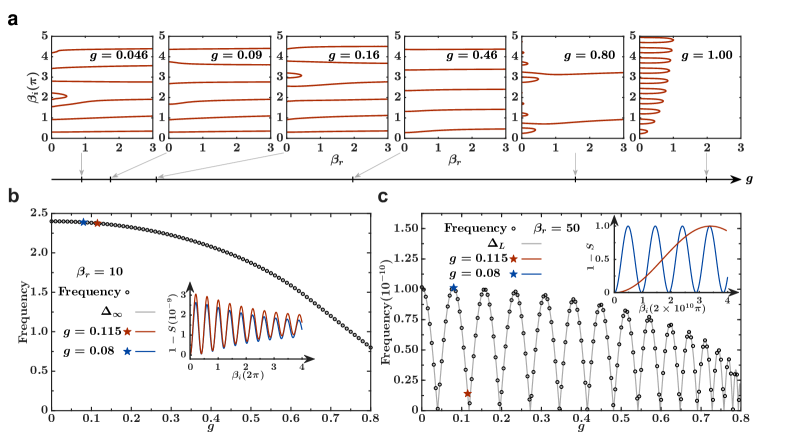
The one-dimensional XY model, beyond its oscillatory phases, embodies characteristics of a ‘Luttinger liquid’ – a fascinating state of matter describing interacting electrons confined to a single dimension. Unlike conventional Fermi liquids, Luttinger liquids exhibit power-law correlations, meaning that properties don’t decay exponentially with distance, but rather follow a slower, power-law dependence. This results in unique behaviors, such as spin-charge separation and a modified density of states, where excitations are no longer simple particle-like entities. The model’s demonstration of these Luttinger liquid properties provides a valuable theoretical platform for understanding a range of physical systems, from quantum wires and carbon nanotubes to the low-energy behavior of certain materials, offering insights into strongly correlated electron systems where traditional approaches fail. Specifically, the observed scaling behavior of quantities like 1/βi0 aligns with predictions based on the Luttinger liquid velocity, further solidifying this connection.
Investigations into the one-dimensional XY model reveal a striking consistency between numerical findings and established theoretical predictions concerning its energetic gaps. Specifically, the oscillation frequency observed in the spin-spin structure factor (SS) precisely aligns with both the calculated thermodynamic limit gap \Delta_\in fty and the finite-size gap \Delta_L. This correspondence serves as strong validation of the analytical results, demonstrating that the model’s behavior is accurately captured by existing theoretical frameworks. The precise matching of these frequencies not only confirms the reliability of the calculations but also offers deeper insight into the nature of the oscillatory phase and the system’s approach to the thermodynamic limit, bolstering confidence in the model’s predictive power.
Analysis reveals a compelling connection between the inverse correlation length, 1/\beta_{i0}, and the underlying physics of the one-dimensional XY model. Specifically, the observed scaling of 1/\beta_{i0} \propto (1-g) directly corresponds to the Van Hove singularity occurring at energy \epsilon_0 = (1-g), indicating a critical point sensitive to the anisotropy parameter. Interestingly, under conditions of low anisotropy (\gamma = 0.1) and large system size (\beta_r = 100), a different scaling relationship emerges: 1/\beta_{i0} \propto \sqrt{1-g^2}. This altered behavior suggests a strong correlation with the velocity of excitations characteristic of a Luttinger liquid, a hallmark of interacting one-dimensional systems, and underscores the model’s ability to capture complex quantum phenomena.
The pursuit of understanding the XY model’s quantum criticality, as demonstrated in this work, necessitates a rigorous analytical approach. One finds echoes of this in Michel Foucault’s assertion: “There is no power relation without resistance.” The complex partition function, employed here to map the phase diagram and reveal spectral weight, functions as a means of ‘resistance’ against the inherent ambiguity of quantum systems. The location of Fisher zeros, critical points in the complex plane, offers a precise, mathematically grounded characterization of the model’s behavior-a stark contrast to purely numerical approximations. The study exemplifies that identifying these ‘zeros’ requires an almost axiomatic precision, echoing a mathematical purity that defines a truly elegant solution.
Where to Next?
The exploration of Fisher zeros, as demonstrated through the lens of the quantum XY chain, has yielded a methodology-not merely a collection of results. The precision with which these zeros map onto spectral features suggests a broader utility, though the reliance on complex partition functions demands careful consideration. One suspects the true elegance lies not in simply finding these zeros, but in predicting their distribution a priori – a mathematically rigorous derivation, rather than a post-hoc confirmation.
A persistent challenge remains the extension of these techniques beyond the relatively tractable one-dimensional systems. The XY model, while serving as a valuable testing ground, ultimately simplifies the complexities inherent in higher dimensions. The emergence of pseudogaps, hinted at by the structure of the Fisher zeros, warrants further investigation – particularly regarding their robustness against perturbations and their potential connection to exotic phases of matter. A proof of universal characteristics, independent of specific model parameters, would elevate this approach beyond a descriptive tool.
Ultimately, the value of this work resides in its insistence on mathematical clarity. The field has, for too long, tolerated approximations and empirical observations. The consistent boundaries and predictability offered by this approach-mapping zeros to physical observables-represent a step towards a more fundamental understanding. The path forward demands not merely the application of these techniques to new systems, but a deepening of the mathematical framework itself.
Original article: https://arxiv.org/pdf/2602.05899.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- Ashes of Creation Rogue Guide for Beginners
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- 10 Most Brutal Acts Of Revenge In Marvel Comics History
- DC K.O.: Superman vs Captain Atom #1 Uses a Fight as Character Study (Review)
- Holstin to be published by Team17
2026-02-06 09:09