Beyond Einstein: Refining Gravity with Scalar Fields

Author: Denis Avetisyan

New research delivers precise calculations of how alternative gravity theories diverge from General Relativity in extreme cosmic scenarios.

In Entangled Relativity, the relative variation of a constant, <span class="katex-eq" data-katex-display="false">\frac{C\_{i}-C\_{0}}{C\_{0}}</span>, is numerically integrated and demonstrably changes with radius, exhibiting a dependency linked to a central density of 100 MeV/fm<span class="katex-eq" data-katex-display="false">^{3}</span>. — In Entangled Relativity, the relative variation of a constant, $\frac{C\_{i}-C\_{0}}{C\_{0}}$ , is numerically integrated and demonstrably changes with radius, exhibiting a dependency linked to a central density of 100 MeV/fm $^{3}$ .

A numerical evaluation of exact Post-Newtonian parameters in Brans-Dicke and Entangled Relativity theories reveals potential observational signatures in strong-field gravity and dipolar gravitational waves.

Standard post-Newtonian approximations in modified gravity theories may fail to capture strong-field effects within compact objects. This is addressed in ‘On the numerical evaluation of the `exact’ Post-Newtonian parameters in Brans-Dicke and Entangled Relativity theories’, where we present novel methods to compute these `exact’ parameters via Tolman-Oppenheimer-Volkoff equations, revealing deviations of over 80% from standard values in certain scenarios. We establish a connection to the $\alpha_{DEF}$ parameter and apply our methodology to both Brans-Dicke theory and Entangled Relativity, deriving parameters for celestial bodies like the Sun, Earth, and neutron stars. Given assumptions about the Lagrangian density, could forthcoming observations-particularly those sensitive to dipolar gravitational waves-finally constrain these alternative theories of gravity?

Beyond Classical Gravity: Mapping the Limits of Einstein’s Theory

Newtonian gravity, despite its enduring success in describing everyday phenomena and even most astronomical motions, fundamentally falters when confronted with the extreme conditions of strong gravitational fields. These breakdowns aren’t merely minor discrepancies; they represent a failure of the theory’s core assumptions regarding spacetime geometry. In regions of intense gravity – such as those surrounding black holes or neutron stars – spacetime itself is significantly warped, requiring a more comprehensive framework like Einstein’s theory of general relativity to accurately model gravitational interactions. The limitations of Newtonian physics in these regimes aren’t theoretical curiosities; they have tangible consequences for understanding the behavior of matter and energy in the most extreme environments of the universe, necessitating the inclusion of relativistic corrections to explain observed phenomena and predict future events.

The refinement of gravitational theory beyond Newton’s law often employs a set of parameters known as Post-Newtonian parameters. These values quantify the deviations from Newtonian gravity in the weak-field regime, meaning situations where gravity is relatively weak and objects move at speeds much slower than the speed of light. This approach doesn’t attempt to create a wholly new theory, but rather builds upon Newtonian gravity through a perturbative expansion-adding increasingly complex terms to correct for relativistic effects. Each parameter represents a specific correction to Newtonian predictions, such as the precession of orbits or the Shapiro delay of light signals. By precisely measuring these parameters through observation and experiment, scientists can test the limits of general relativity and search for potential modifications to Einstein’s theory, effectively mapping the subtle ways gravity deviates from its classical description.

The conventional framework for refining Newtonian gravity relies on parameters designed for scenarios with relatively weak gravitational fields and slow-moving objects; however, this approach encounters limitations when applied to extreme astrophysical environments. Recent calculations demonstrate that the post-Newtonian parameter γ, which measures the degree of gravitational polarization, can deviate from unity by as much as 16.1% within the intense gravitational field of a neutron star. This significant departure from expected values highlights the inadequacy of perturbative approximations in strong-field regimes and underscores the necessity for more robust theoretical models capable of accurately describing gravity where fields are intense and velocities approach a substantial fraction of the speed of light. These findings suggest that a complete understanding of phenomena like gravitational waves emitted from compact objects demands a move beyond the standard weak-field approximations.

A plot of relative differences between exact and standard post-Newtonian γ parameters, computed across a range of ω values (from <span class="katex-eq" data-katex-display="false">10^{-1}</span> to <span class="katex-eq" data-katex-display="false">10^{6}</span>) and central densities (from 100 to 1570 MeV/fm<span class="katex-eq" data-katex-display="false">^{3}</span>), reveals the deviation in percent between the two definitions, constrained by a speed of sound limit of <span class="katex-eq" data-katex-display="false">c/\sqrt{3}</span> to ensure physical consistency (Bedaque and Steiner, 2015). — A plot of relative differences between exact and standard post-Newtonian γ parameters, computed across a range of ω values (from $10^{-1}$ to $10^{6}$ ) and central densities (from 100 to 1570 MeV/fm $^{3}$ ), reveals the deviation in percent between the two definitions, constrained by a speed of sound limit of $c/\sqrt{3}$ to ensure physical consistency (Bedaque and Steiner, 2015).

Entangled Spacetime: A Novel Framework for Gravitational Interaction

Entangled Relativity departs from the traditional understanding of gravity as solely a geometric property of spacetime described by Einstein’s field equations. Instead, it posits a non-linear coupling between matter and the underlying geometry, meaning the influence of matter on spacetime is not proportional to its energy-momentum tensor in a simple, fixed relationship. This non-linearity arises from the framework’s core principle: gravity isn’t merely in spacetime, but is fundamentally entangled with the quantum states of matter. Consequently, the gravitational field itself acquires degrees of freedom beyond those predicted by general relativity, potentially leading to observable deviations in strong gravitational regimes and modifications to gravitational wave propagation. The mathematical formulation necessitates considering higher-order curvature terms and interactions beyond the standard $R_{\mu\nu} - \frac{1}{2}g_{\mu\nu}R$ action, thereby requiring alternative approaches to solving for spacetime metrics.

Entangled Relativity posits that gravitational interactions are mediated by a scalar field, φ, distinct from the tensor-based description of General Relativity. This scalar field couples to matter and, crucially, to itself, introducing non-linearities absent in the Einstein field equations. Consequently, solutions to this framework predict deviations from General Relativity, including modified gravitational potentials and the potential for scalar gravitational waves. These deviations manifest as alterations to the spacetime metric and can lead to observable phenomena such as variations in planetary orbits, differing gravitational lensing effects, and the existence of fifth forces detectable in precision experiments. The strength of the coupling between the scalar field and matter is a free parameter, allowing for tunable deviations and offering a potential explanation for dark matter and dark energy without requiring their explicit introduction.

Modeling exterior spacetime within the Entangled Relativity framework necessitates advanced techniques due to the non-linear nature of the field equations. The Janis-Newman-Winicour (JNW) metric provides a systematic method for generating exact solutions, particularly those representing localized sources like stars or black holes. This approach involves applying specific transformations to known solutions of Einstein’s field equations – most commonly the Schwarzschild or Kerr metrics – to incorporate the scalar field mediating gravity in this model. The JNW method allows researchers to construct solutions exhibiting deviations from general relativity, facilitating the investigation of potential observational signatures and testing the validity of the Entangled Relativity framework. Specifically, the JNW algorithm relies on a series of algebraic manipulations and substitutions to obtain solutions that satisfy the modified field equations, ensuring consistency with the underlying theoretical principles.

Compact Star Structure: Relativistic Hydrostatics and the TOV Equations

The Tolman-Oppenheimer-Volkoff (TOV) equations are a set of stellar structure equations describing a spherically symmetric, static, and perfect fluid star in general relativity. These equations represent a relativistic generalization of the Newtonian hydrostatic equilibrium, accounting for gravitational effects beyond the Newtonian approximation. Specifically, the TOV equations relate the pressure gradient to the gravitational mass within the star, allowing for the determination of the star’s internal structure given an equation of state. The primary equation, derived from Einstein’s field equations, is $dP/dr = - \frac{G m(r) \rho(r)}{r^2} \left( 1 + \frac{P(r)}{\rho(r)} \right)$ , where $P$ is pressure, ρ is density, $m(r)$ is the mass enclosed within radius $r$ , and $G$ is the gravitational constant. Solving the TOV equations, along with the equation of state and appropriate boundary conditions, yields the star’s mass and radius profiles, and determines the maximum mass a star of a given composition can support before collapsing into a black hole.

Within the framework of Entangled Relativity, the Tolman-Oppenheimer-Volkoff (TOV) equations are modified to incorporate a scalar field, allowing for investigation of its influence on neutron star characteristics. The scalar field introduces an additional pressure term and alters the gravitational mass, impacting both the maximum mass and radius achievable by a neutron star before collapse. Solutions to the modified TOV equations demonstrate that the presence of the scalar field generally leads to a reduction in the maximum mass compared to standard general relativity calculations, while the effect on the radius is more complex and depends on the specific parameters of the scalar field. This interaction between the scalar field and the stellar matter provides a mechanism for probing the fundamental properties of the field and testing alternative theories of gravity in the strong-field regime of neutron stars.

Solutions to the Tolman-Oppenheimer-Volkoff equations, when calculated within the framework of Entangled Relativity, yield $Exact Post-Newtonian Parameters$ that remain valid under the extreme gravitational conditions found within neutron stars – a regime where standard approximations break down. Analysis demonstrates that the parameter δ_exact, representing a key measure of spacetime curvature, can deviate from unity by as much as 40.1% for neutron stars. This substantial deviation highlights the importance of incorporating strong-field corrections into models of compact stars and validates the necessity of utilizing exact solutions, rather than relying on perturbative approximations, to accurately predict their properties and behavior.

The rate of change of the predicted proper motion <span class="katex-eq" data-katex-display="false">\dot{P}^{D}</span> correlates with the estimated masses of neutron stars, exhibiting distinct behaviors for different equations of state. — The rate of change of the predicted proper motion $\dot{P}^{D}$ correlates with the estimated masses of neutron stars, exhibiting distinct behaviors for different equations of state.

Gravitational Waves and the Search for New Physics

The universe offers a subtle yet powerful means of testing the fundamental laws of gravity through the observation of dipolar gravitational waves. Unlike the dominant quadrupolar waves produced by symmetrical events, these waves originate from systems with asymmetric mass distributions – think of a star with a significant bulge or an unevenly rotating neutron star. These asymmetries generate a distinct gravitational signature that deviates from the predictions of general relativity, providing a crucial window into modified gravity theories. By meticulously analyzing the characteristics of these waves, such as their amplitude and polarization, scientists can probe the validity of alternative gravitational models and search for evidence of new physics beyond Einstein’s established framework. The detection and characterization of dipolar gravitational waves, therefore, represent a unique and potentially revolutionary approach to understanding the very fabric of spacetime.

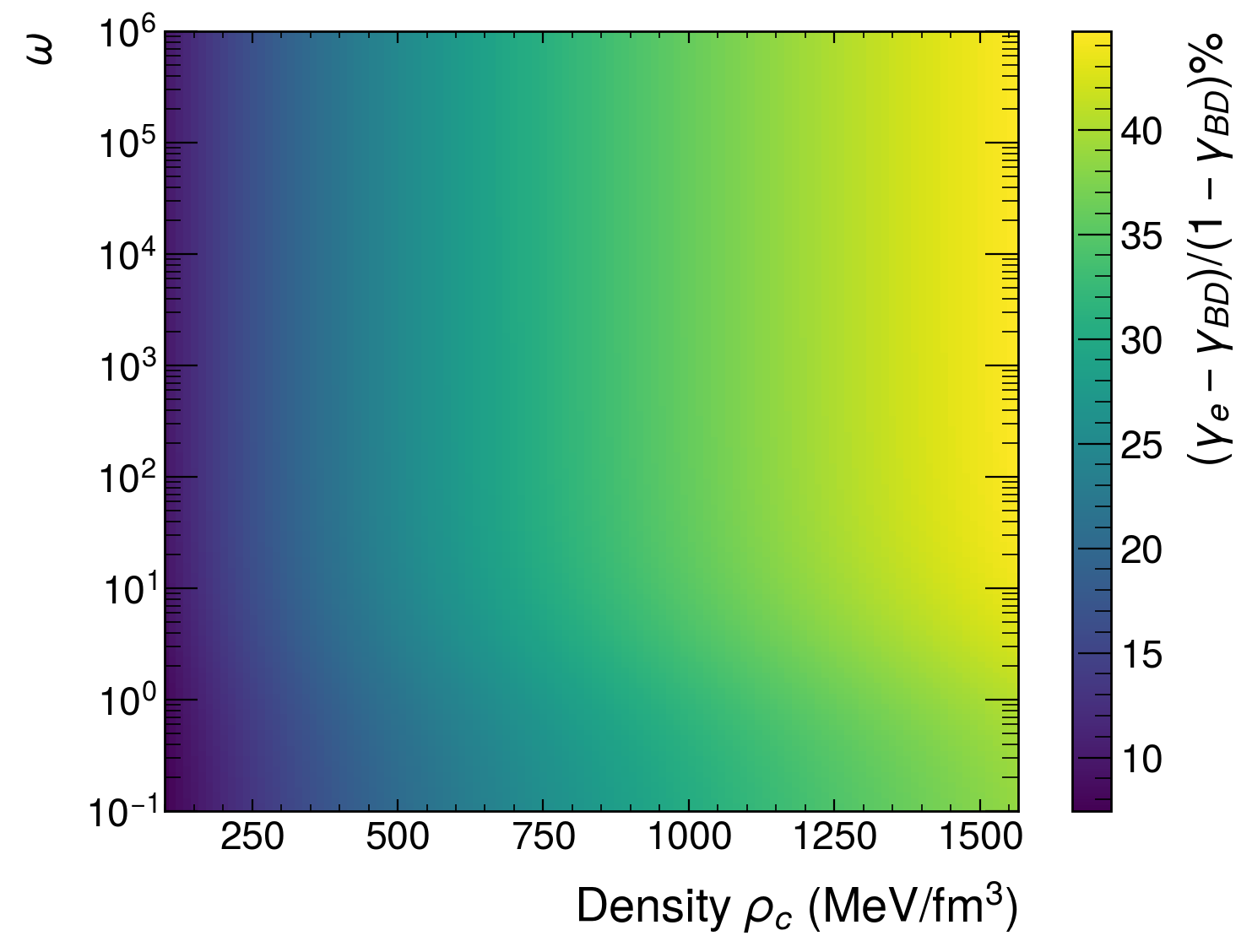
The intensity of dipolar gravitational waves, a potential signature of physics beyond Einstein’s general relativity, is quantified by the Damour-Esposito-Farèse (DEF) parameter. This parameter effectively measures the degree to which gravity deviates from its standard formulation, specifically relating to the theory’s preferred frame effects. Current observational efforts, primarily through the analysis of binary pulsar timing and gravitational wave detectors, aim to constrain the DEF parameter. A precise determination of this value allows scientists to test the validity of alternative gravity theories – those proposing modifications to general relativity – by comparing theoretical predictions with empirical data. Even null results – tight constraints on the DEF parameter – are valuable, as they progressively narrow the range of viable alternative theories and refine the search for new physics governing the universe.

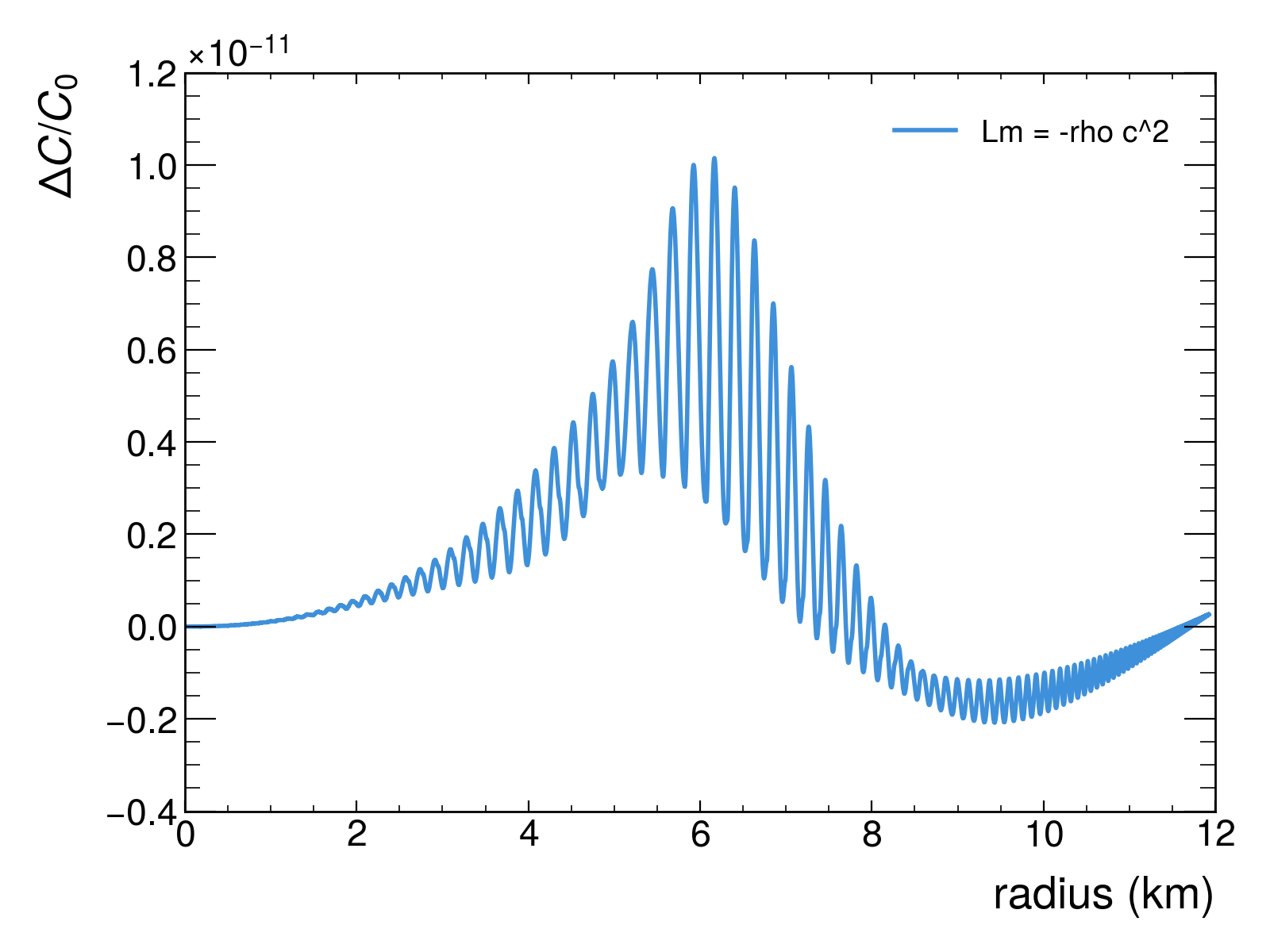
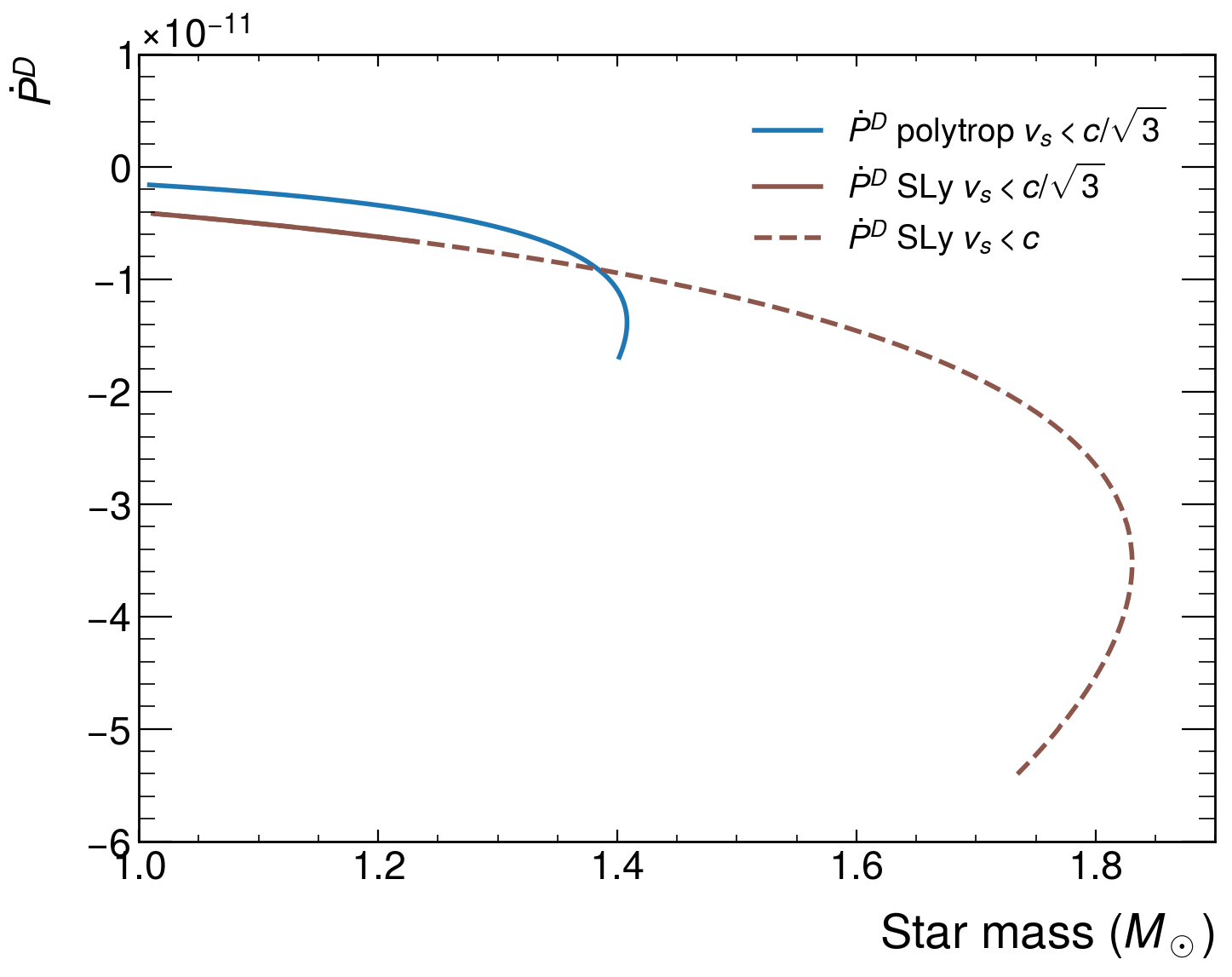
The ongoing detection of gravitational waves provides a powerful means to rigorously test the foundations of gravity itself, extending beyond the well-established predictions of general relativity. Current research focuses on comparing theoretical waveforms – the ‘fingerprints’ of merging cosmic events – with those actually observed by detectors like LIGO and Virgo. Specifically, investigations into alternative theories such as Entangled Relativity predict measurable deviations in the orbital period of binary systems, expressed as $\dot{P}$ , which represents the rate of change in the orbital period. Calculations indicate a predicted range of $-1.69 \times 10^{-{11}} \text{ s/s}$ to $-1.62 \times 10^{-{12}} \text{ s/s}$ for this variation – a magnitude significantly exceeding current observational limits. This discrepancy potentially invalidates certain assumptions within these theories, notably the condition $\mathcal{L}_m = -\rho$ , and opens avenues for exploring new physics that could reshape our understanding of the universe’s fundamental forces.

The pursuit of exact solutions within modified gravity theories, as demonstrated by this evaluation of Post-Newtonian parameters in Brans-Dicke and Entangled Relativity, reveals a delicate interplay between theoretical structure and observational consequence. The study highlights how deviations from General Relativity become increasingly pronounced in strong-field regimes, demanding rigorous numerical analysis to connect theory with potential dipolar gravitational wave signatures. This mirrors a fundamental principle of systemic understanding: structure dictates behavior. As Carl Sagan once observed, “Somewhere, something incredible is waiting to be known.” The work embodies this sentiment, meticulously probing the theoretical landscape to uncover subtle, yet potentially revolutionary, predictions about the universe’s gravitational nature.

Where Do We Go From Here?

The pursuit of precision in modified gravity, as demonstrated by this work, inevitably circles back to a fundamental question: what are we actually optimizing for? The numerical evaluation of post-Newtonian parameters, while technically demanding, is merely a means to an end. It exposes deviations from General Relativity, but those deviations are only meaningful if linked to observable phenomena – and, crucially, if those phenomena are understood with sufficient clarity to discern a signal from noise. The potential for dipolar gravitational waves offers such a path, yet the true sensitivity required to detect them remains a significant hurdle.

It is tempting to view scalar-tensor theories as a search for ‘better’ gravity. However, a more honest assessment reveals a quest for a complete gravity – one that gracefully incorporates the observed acceleration of the universe and avoids the need for ad-hoc dark energy. Simplicity, in this context, is not minimalism, but the discipline of distinguishing the essential from the accidental. The Tolman-Oppenheimer-Volkoff equation, while a cornerstone of neutron star modeling, reveals the limitations of static, spherically symmetric approximations. Future work must embrace fully dynamic, multi-dimensional simulations to truly probe the strong-field regime.

The enduring challenge lies not in calculating parameters, but in designing experiments that can meaningfully constrain them. The theoretical landscape is replete with models; the observational universe will be the ultimate arbiter. The refinement of these calculations, therefore, is not an end in itself, but a necessary step toward a deeper understanding of the universe’s fundamental structure and its governing principles.

Original article: https://arxiv.org/pdf/2602.11811.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Beyond Classical Gravity: Mapping the Limits of Einstein’s Theory

Entangled Spacetime: A Novel Framework for Gravitational Interaction

Compact Star Structure: Relativistic Hydrostatics and the TOV Equations

Gravitational Waves and the Search for New Physics

Where Do We Go From Here?

See also: