Beyond Neutron Stars: Unlocking the Secrets of Ultra-Dense Matter

Author: Denis Avetisyan

New research draws parallels between ultracold atoms and the exotic states of matter found in neutron stars to explain the transition between hadronic and quark-dominated phases.

Calculated momentum distributions reveal how quark-like fermions <span class="katex-eq" data-katex-display="false">f_Q(k)</span> and baryon-like trimers <span class="katex-eq" data-katex-display="false">f_B(K)</span> respond to variations in <span class="katex-eq" data-katex-display="false">\mu/T</span>, with behavior anchored by the Fermi momentum <span class="katex-eq" data-katex-display="false">k_F = \sqrt{2m\mu}</span> at a fixed temperature of <span class="katex-eq" data-katex-display="false">T = 0.1\mathcal{B}</span>. — Calculated momentum distributions reveal how quark-like fermions $f_Q(k)$ and baryon-like trimers $f_B(K)$ respond to variations in $\mu/T$ , with behavior anchored by the Fermi momentum $k_F = \sqrt{2m\mu}$ at a fixed temperature of $T = 0.1\mathcal{B}$ .

This review explores the emergence of quarkyonic matter and the hadron-quark crossover, proposing that tripling fluctuations of baryons, analogous to the BEC-BCS crossover, drive the observed peaked speed of sound in dense matter.

The dense matter equation of state remains a fundamental challenge in astrophysics, particularly in understanding the transition between hadronic and quark matter within neutron stars. This work, ‘Quarkyonic matter and hadron-quark crossover from an ultracold atom perspective’, proposes a novel mechanism for this hadron-quark crossover, drawing parallels with the Bose-Einstein condensate to Bardeen-Cooper-Schrieffer (BEC-BCS) transition observed in ultracold atomic gases. Specifically, we demonstrate that tripling fluctuations of baryons can simultaneously explain the predicted peak in the speed of sound and the emergence of quarkyonic matter-a phase characterized by a distinct momentum-shell structure. Could this framework, rooted in the physics of many-body quantum systems, offer a crucial step toward a microscopic understanding of dense matter’s behavior?

The Echo of Collapse: Probing Matter’s Final Form

The extreme densities found within neutron stars – remnants of collapsed stars containing masses greater than the sun compressed into a sphere only twenty kilometers across – pose a significant challenge to contemporary nuclear physics. At such densities, the very fabric of matter undergoes transformations, exceeding anything achievable in terrestrial laboratories. Protons and neutrons are no longer distinct entities, but rather exist within a superfluid ‘soup’ where the strong nuclear force dominates. Accurately describing this state requires going beyond conventional models, as the behavior of matter under these conditions dictates not only the structure and evolution of neutron stars, but also provides insights into the fundamental nature of quantum chromodynamics – the theory governing the strong force. Understanding this dense matter equation of state is crucial for deciphering the properties of these enigmatic celestial objects and probing the limits of our knowledge about the universe.

Conventional methods in nuclear physics, such as basic Mean-Field Theory, struggle to fully represent the behavior of matter at extreme densities because they often simplify the interactions between particles. These theories typically treat particles as moving in an average potential, effectively smoothing out the inherent quantum fluctuations that become incredibly important under immense pressure. In reality, particles within neutron stars, for example, don’t move in a static field; instead, they constantly interact, creating temporary, localized variations in density and momentum. Capturing these fluctuation effects-the correlated motions and temporary groupings of particles-is essential for accurately predicting the equation of state of dense matter and, consequently, the properties of neutron stars. Ignoring these fluctuations can lead to significant errors in calculations, particularly when approaching the transition to exotic states of matter like quark matter, where collective effects become dominant.

The ultimate fate and observed characteristics of neutron stars hinge on a precise understanding of the Hadron-Quark Crossover – the dramatic shift in matter’s composition at immense densities. Within these stellar remnants, matter isn’t simply compressed atomic nuclei; at a critical point, hadrons – protons and neutrons – are theorized to dissolve into their constituent quarks, transitioning into a fundamentally different state. Accurately modeling this crossover is exceptionally difficult because it doesn’t represent a sharp phase transition, but rather a gradual change influenced by complex interactions and quantum fluctuations. The exact nature of this transition – whether it’s a smooth crossover, a sharp phase transition, or something more exotic – directly impacts properties like the star’s radius, mass, and cooling rate, and remains a central puzzle in modern nuclear physics. Current theoretical models struggle to reconcile predictions with observational data, demanding innovative approaches to capture the intricacies of matter at these extreme densities.

A Symphony of Correlation: Tripling Fluctuation Theory Emerges

Tripling Fluctuation Theory represents an advancement in modeling the Hadron-Quark Crossover by addressing limitations inherent in mean-field approximations. Traditional mean-field approaches often simplify complex many-body interactions, neglecting crucial correlations between baryons. This theory explicitly incorporates these baryon correlations, recognizing that the collective behavior of these particles significantly influences the transition between hadronic and quark-gluon plasma phases. By moving beyond the single-particle picture, Tripling Fluctuation Theory provides a more accurate description of the crossover, enabling predictions of novel states of matter and refining the understanding of extreme density environments, such as those found in neutron stars and heavy-ion collisions.

Tripling Fluctuation Theory models the Hadron-Quark Crossover by explicitly incorporating baryon correlations, addressing limitations found in mean-field approximations which typically treat baryons independently. This approach recognizes that at high densities, baryons exhibit collective behavior due to their strong interactions. The theory utilizes the Phase-Shift Representation to characterize these interactions, allowing for a precise calculation of scattering amplitudes and correlation functions. This representation effectively describes how baryons scatter off each other, influencing the overall thermodynamic properties of the system and enabling the prediction of novel phases of matter. By accurately capturing these multi-particle correlations, the theory goes beyond single-particle approximations and provides a more realistic depiction of the system’s behavior.

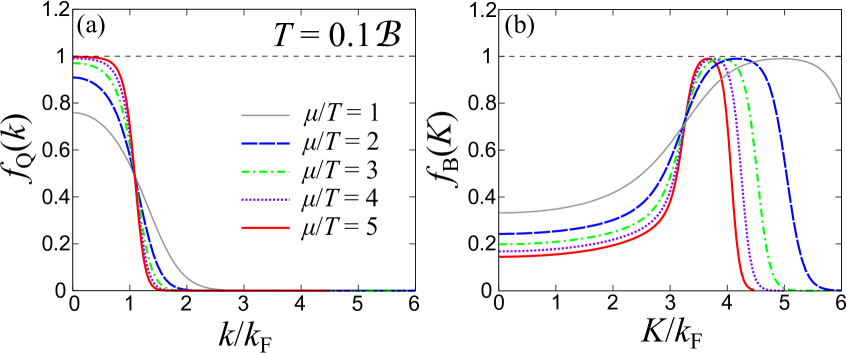
Tripling Fluctuation Theory predicts the existence of Quarkyonic Matter, a state characterized by a distinct Baryonic Momentum Shell. The width of this shell, denoted as ΔB, is quantitatively determined by the equation $ΔB = \sqrt(2MB(Ncμ - Ncmq + ℬ)) - \sqrt(2MB Nc(μ - mq))$ , where M represents the baryon mass, N_c is the number of colors, μ is the baryonic chemical potential, m_q is the quark mass, and ℬ is a parameter accounting for interactions. This formulation allows for a precise calculation of the momentum range occupied by baryons within the Quarkyonic phase, differentiating it from other predicted phases of QCD matter and providing a testable prediction for experimental verification via heavy-ion collision data.

The development of Tripling Fluctuation Theory benefits from established theoretical frameworks used to describe the BEC-BCS crossover in ultracold Fermi gases. This crossover describes the transition between a Bardeen-Cooper-Schrieffer (BCS) superfluid, characterized by wide separation of Cooper pairs, and a Bose-Einstein Condensate (BEC) of tightly bound bosons. Analogous to the formation of Cooper pairs, Tripling Fluctuation Theory models the correlated formation of baryons at high density. The mathematical techniques developed for the BEC-BCS crossover, particularly those concerning effective potential calculations and the treatment of fluctuations around mean-field solutions, are directly applicable to understanding the Hadron-Quark crossover and predicting novel phases like Quarkyonic Matter. This shared theoretical ground allows for the transfer of computational methods and provides a robust validation framework for the new theory.

Echoes of a Phase Transition: The Speed of Sound as a Diagnostic

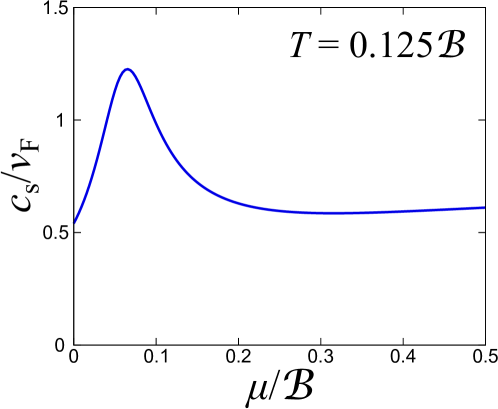
Tripling Fluctuation Theory predicts a characteristic Speed of Sound Peak within the equation of state as the system transitions from hadronic matter to a Quark-Gluon Plasma. This peak manifests as a local maximum in $c_s^2$ , where $c_s$ represents the speed of sound. The equation of state relates pressure to energy density, and the speed of sound is derived from it. The theoretical basis posits that fluctuations in baryon number density, specifically tripling fluctuations, influence the equation of state, creating this discernible peak. This peak is not a feature of conventional fluids and serves as a unique signature of the Hadron-Quark Crossover, distinguishing it from a simple phase transition.

The Speed of Sound Peak observed in the equation of state during the Hadron-Quark Crossover is directly attributable to an increase in the system’s compressibility. As the transition from hadronic to quark matter occurs, the interactions between constituent particles are modified, leading to a softening of the equation of state. This softening manifests as a decreased resistance to compression, effectively increasing the compressibility of the system. The enhanced compressibility allows for faster propagation of sound waves – hence the peak – and is a key signature of the changing inter-particle dynamics at the crossover point. $c_s^2 = \frac{dP}{d\epsilon}$ , where $c_s$ is the speed of sound, $P$ is the pressure, and ε is the energy density, demonstrates how a change in the pressure-energy density relationship directly impacts sound propagation.

Empirical data from heavy-ion collision experiments, alongside lattice quantum chromodynamics (LQCD) simulations, consistently reveal a pronounced peak in the speed of sound at energies relevant to the Hadron-Quark Crossover. This peak is directly correlated with the suppression of low-momentum baryon distributions, a consequence of tripling fluctuations in baryon number density. The observed behavior exhibits a strong analogy to the Bose-Einstein Condensation-Bardeen-Cooper-Schrieffer (BEC-BCS) crossover in condensed matter physics, where a similar suppression of low-momentum particles occurs due to pairing effects; the suppression in the hadronic phase arises from the formation of color-flavor locked phases. Quantitative analysis of these simulations confirms the theoretical prediction of an increase in compressibility around the transition temperature, manifesting as the observed peak in the speed of sound $c_s^2$ .

The observation of the Speed of Sound Peak, consistent with Tripling Fluctuation Theory, provides constraints on the equation of state (EoS) of dense baryonic matter, directly impacting our understanding of neutron star composition. Neutron stars, possessing densities exceeding those achievable in terrestrial experiments, require accurate EoS models to predict observable properties such as mass-radius relationships and gravitational wave signals. The EoS derived from observations confirming the Speed of Sound Peak allows for refined modeling of neutron star interiors, particularly the behavior of matter at supranuclear densities. Specifically, it supports scenarios involving exotic forms of matter, like hyperons or quark matter, and constrains the parameters governing their interactions, thereby reducing uncertainties in neutron star structure and evolution calculations.

At a temperature of <span class="katex-eq" data-katex-display="false">T=0.125\mathcal{B}</span>, the normalized isothermal speed of sound <span class="katex-eq" data-katex-display="false">c_s</span> scales with the Fermi velocity <span class="katex-eq" data-katex-display="false">v_F = k_F/m</span>. — At a temperature of $T=0.125\mathcal{B}$ , the normalized isothermal speed of sound $c_s$ scales with the Fermi velocity $v_F = k_F/m$ .

Beyond the Stellar Core: A Wider Resonance

Tripling Fluctuation Theory, initially developed to probe the exotic conditions within neutron stars, represents a significant advancement in the broader study of strongly interacting systems. This approach doesn’t limit itself to astronomical objects; instead, it provides a powerful framework for understanding any system where particles interact intensely, such as those encountered in high-energy nuclear collisions or even within certain condensed matter materials. By meticulously accounting for fluctuations in particle number – specifically, considering groupings of three particles – the theory offers a more nuanced and accurate description of collective behavior than traditional methods. This refinement allows physicists to predict and interpret phenomena arising from these strong interactions with increased precision, ultimately fostering a deeper understanding of the fundamental forces governing matter at its most basic level. The theory’s versatility highlights its potential to unlock insights across diverse areas of physics, extending far beyond its initial application to the extreme environment of a neutron star.

The theoretical advancements stemming from Tripling Fluctuation Theory aren’t limited to the extreme conditions within neutron stars; they significantly refine the broader understanding of phase transitions across numerous physical systems. Building upon the established Nozières-Schmitt-Rink Approach, this framework provides a more nuanced description of how matter transforms between different states – solid to liquid, or even in the complex realm of superconductivity. By accurately capturing the fluctuations that precede and define these transitions, the theory moves beyond simple order parameters, offering a detailed picture of the critical phenomena occurring at a microscopic level. This improved resolution isn’t merely academic; it has implications for materials science, condensed matter physics, and potentially even the study of the early universe, where phase transitions played a crucial role in shaping the cosmos.

The developed theoretical framework leverages the established principles of Quantum Chromodynamics (QCD), the fundamental theory describing the strong force, and extends its reach through the simplification of Two-Color QCD. This approach allows researchers to probe extreme conditions – such as those found in the cores of neutron stars or created in heavy-ion collisions – and predict the emergence of novel states of matter beyond the familiar solid, liquid, or gas phases. By systematically investigating how quarks and gluons interact under immense pressure and temperature, the framework offers insights into the properties of these exotic phases, including their viscosity, equation of state, and potential for superconductivity. This capability is not limited to astrophysical contexts; it also provides a pathway for understanding complex phenomena in condensed matter physics and potentially guiding the design of materials with unprecedented characteristics.

The resonance of Tripling Fluctuation Theory with both neutron star physics and broader strongly interacting systems highlights a crucial principle: theoretical advancements needn’t be confined by disciplinary boundaries. By successfully applying concepts originating in Quantum Chromodynamics – and refined through models like the Nozières-Schmitt-Rink Approach – to seemingly unrelated areas of nuclear physics, this framework showcases the interconnectedness of fundamental forces. This cross-pollination of ideas isn’t merely a methodological triumph; it suggests that shared underlying principles govern diverse phenomena, opening avenues for novel insights. The ability to leverage tools developed for one extreme environment-like the ultra-dense core of a neutron star-to illuminate the behavior of matter in others signals a powerful trend in modern physics, promising future breakthroughs in understanding the universe’s most complex systems and potentially revealing entirely new states of matter.

The pursuit of understanding dense matter, as outlined in this exploration of the hadron-quark crossover, resembles tending a complex garden. One seeks not to build a definitive picture, but to cultivate conditions where emergent properties-like the peaked speed of sound-can flourish. It recalls John Stuart Mill’s observation that “The only freedom which deserves the name is that of pursuing truth, unhindered by any consideration.” This research doesn’t impose a structure, but allows the system-baryonic matter under extreme pressure-to reveal its inherent organization through tripling fluctuations, much like observing the natural order within a thriving ecosystem. The goal isn’t control, but understanding the delicate balance that gives rise to phenomena such as the formation of quarkyonic matter.

The Shape of Things to Come

The pursuit of the hadron-quark crossover, framed through the lens of ultracold atomic systems, reveals a truth often obscured by the desire for neat phase transitions: systems don’t have transitions, they become other systems. This work, by identifying tripling fluctuations as potentially emergent from a BEC-BCS-like mechanism, doesn’t solve the riddle of quarkyonic matter – it simply shifts the problem. Long stability of a predicted speed of sound peak is not confirmation, but a prophecy of the unexpected ways this system will deviate as density increases-the very conditions where our analogies begin to fray.

The true challenge lies not in reproducing existing observations, but in predicting the qualitative changes beyond the reach of current theoretical tools. Focusing solely on microscopic origins, while valuable, risks overlooking the macroscopic feedback loops that will inevitably dominate at the extreme densities found within neutron stars. The question isn’t simply how does hadronic matter transition, but what does it become when it resists such categorization?

Future investigations should embrace the inherent messiness of strongly correlated systems, acknowledging that the search for a ‘crossover’ is, at best, a temporary respite from the inevitable emergence of entirely novel states of matter. The elegance of the BEC-BCS analogy shouldn’t blind anyone to the fact that real stars are not laboratory experiments. They are chaotic, evolving ecosystems, and their interiors will, in the end, reveal surprises no amount of theoretical foresight can fully anticipate.

Original article: https://arxiv.org/pdf/2602.14113.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Echo of Collapse: Probing Matter’s Final Form

A Symphony of Correlation: Tripling Fluctuation Theory Emerges

Echoes of a Phase Transition: The Speed of Sound as a Diagnostic

Beyond the Stellar Core: A Wider Resonance

The Shape of Things to Come

See also: