Beyond Entanglement: A New Path to Quantum Many-Body Solutions

Author: Denis Avetisyan

Researchers demonstrate a novel wavefunction ansatz, leveraging product state superpositions, for efficient ground state searches in quantum spin systems.

The study demonstrates the trainability of a specific parameterized quantum ansatz—the Symmetry Preserving Ansatz (SPS)—by showing that gradients of local observables with respect to variational parameters remain well-behaved across numerous random samples and system sizes, avoiding the problematic “barren plateaus” that hinder optimization in large quantum systems; specifically, gradient uniformity is observed for coefficient parameters, localization for site indices, and variances that decrease with system size and scale polynomially with the number of product states, suggesting efficient optimization is achievable even for complex quantum simulations.

This work introduces and analyzes the Superposition of Product States (SPS) ansatz, showcasing its trainability, expressiveness, and scalability as a variational wavefunction for tackling complex quantum problems.

Despite the established success of tensor networks in modeling one-dimensional quantum systems, extending these methods to higher dimensions remains challenging due to limitations in expressive power and information extraction. This work, ‘Exploring the performance of superposition of product states: from 1D to 3D quantum spin systems’, investigates the superposition-of-product-states (SPS) ansatz as a geometrically independent and readily parallelizable variational wavefunction. We demonstrate that SPS exhibits favorable trainability, achieves high accuracy in ground state searches across diverse spin models—including one-, two-, and three-dimensional systems with both short- and long-range interactions—and offers analytical advantages over traditional tensor network approaches. Could this ansatz provide a viable pathway toward scalable variational quantum algorithms for complex many-body problems?

The Illusion of Expressibility

Quantum many-body problems pose a significant computational challenge due to exponential scaling. Traditional methods quickly become intractable, hindering progress in materials science and condensed matter physics. Variational methods offer a promising approach by approximating the ground state using a parameterized ansatz, reducing the problem to an optimization task. The key lies in balancing expressibility—the ability to represent complex states—and computational tractability. The superposition-of-product-states (SPS) ansatz demonstrates initial promise, but every elegant theory seems destined to meet the harsh realities of production.

Taming Complexity with Tensor Networks

Tensor network algorithms provide a powerful framework for representing quantum states with interconnected tensors, enabling simulations of otherwise intractable systems. This approach decomposes high-dimensional states into lower-dimensional tensors, significantly reducing computational cost. These methods exploit correlations to truncate the Hilbert space, proving effective for systems with limited entanglement. Techniques like CornerTransferMatrixRenormalizationGroup and BoundaryMPS extend these capabilities, with SPS often performing comparably to DMRG. These advancements broaden applicability to a wider range of physical problems.

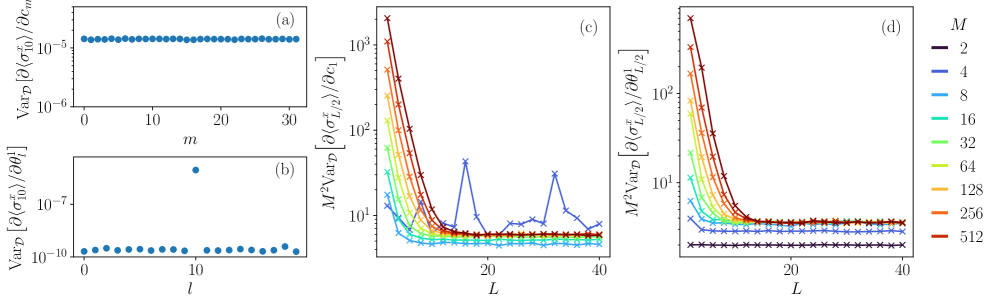
The Optimization Minefield: Barren Plateaus

Optimizing variational ansatz parameters is crucial for accurate results. However, high-dimensional parameter spaces are often riddled with barren plateaus—regions where gradients vanish, stalling optimization. This phenomenon arises from exponentially decreasing gradient norms as system size increases, hindering scalability. Concepts like RestrictedTypicality aim to address this by identifying robust ansätze. The Symmetry Preserving Ansatz (SPS) mitigates the barren plateau problem, exhibiting polynomially decreasing gradient variance with system size, unlike many other approaches.

Stress-Testing Algorithms: Beyond Simple Models

The TiltedIsingModel, with extensions to RandomCouplingNetwork configurations and long-range interactions, serves as a valuable benchmark for quantum algorithms. This model’s adaptability allows systematic investigation of scalability and accuracy. Density Matrix Renormalization Group (DMRG) successfully simulates these models, demonstrating the effectiveness of tensor networks. Understanding the interplay between model complexity and algorithm performance is critical. The SPS ansatz achieves relative errors as low as $10^{-8}$ for ground-state approximations, highlighting the potential for accurate simulations. Ultimately, every elegant solution is just a temporary reprieve.

The Underlying Math and Future Directions

Variational quantum algorithms rely on parameterized quantum circuits, or ansätze, to approximate ground states. Their effectiveness is linked to the mathematical properties of the ansatz, often rooted in CanonicalPolyadicDecomposition. Characterizing entanglement structure is crucial for designing effective ansätze; measures like 2RenyiEntropy provide valuable insights.

Figure 3:Typical 2-Rényi entropies obtained from 10,000 random SPS samples. (a) The distribution of the typical 2-Rényi entropies forL=20L=20. The entropies typically concentrate far from the theoretical maximum, even asMMincreases. (b) The minimum relative errors from the theoretical maximum saturate for largerLL.

Exploring NeuralQuantumStates and other machine learning-inspired approaches offers exciting possibilities. The Specific Polynomial Structure (SPS) ansatz exhibits a computational scaling of $O(LM^2)$ for local observable computation, enabling efficient simulations. Future research will likely focus on hybrid quantum-classical algorithms leveraging the strengths of both machine learning and quantum computation.

The pursuit of elegant solutions in quantum computation invariably courts practical limitations. This paper’s exploration of the Superposition of Product States (SPS) ansatz, while theoretically promising for ground state searches, feels less like a breakthrough and more like a temporary reprieve. As with all variational methods, the ansatz’s ultimate utility hinges on its trainability—a quality perpetually under siege by the realities of optimization landscapes. It’s a familiar pattern: a framework designed to simplify the search for quantum states inevitably encounters the complexities of implementation. As John Bell once observed, “No physicist believes that mechanism is anything but an approximation.” The SPS ansatz may offer analytical tractability, but production environments will undoubtedly reveal unforeseen constraints and scaling challenges, adding another layer to the already substantial tech debt.

What’s Next?

The enthusiastic embrace of variational methods continues, predictably. This Superposition of Product States ansatz, with its convenient analytical tractability, feels… tidy. Too tidy, perhaps. The paper demonstrates ground state searches; production systems will demand searches for excited states, and then demand to know why the algorithm insists on finding states that violate conservation laws. One suspects the scaling arguments, currently so promising, will encounter the usual friction when applied to Hamiltonians bearing even a passing resemblance to reality.

The authors rightly emphasize trainability, but trainability is merely a delay of the inevitable. Any wavefunction called ‘expressive’ simply hasn’t been subjected to enough gradient descent. The real question isn’t whether this ansatz can represent the ground state, but how much computational effort is required to coax it into doing so, and how gracefully it fails when presented with a problem it was never designed to solve. Better one well-understood parameter than a thousand that mysteriously vanish during optimization.

The inevitable extension to three dimensions is sketched, and one anticipates the corresponding increase in computational complexity. The authors hint at connections to tensor networks; these are, of course, just another way to avoid actually solving the Schrödinger equation. The field chases increasingly elaborate methods; the logs, however, remain stubbornly consistent.

Original article: https://arxiv.org/pdf/2511.08407.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/