Beyond the Standard Model: The Spectroscopic Search for New Physics
![Precision spectroscopy, applied across diverse atomic, molecular, and exotic systems-including hydrogenic atoms, molecular ions, and muonium-establishes a complementary sensitivity to new physics, with the reach dependent on specific combinations of effective couplings to fundamental particles and modulated by the characteristic interaction range, as evidenced by the distinct sectors delineating sensitivity for electrons, muons, protons, and neutrons [latex] [/latex].](https://arxiv.org/html/2602.20750v1/x2.png)
Atomic and molecular spectroscopy are emerging as powerful tools to explore phenomena beyond our current understanding of the universe.
Science
Quantum Islands: Engineering Exotic Anyons in Fractional Hall States
![Spherical braids, closely related to traditional Artin braids, differ in a crucial topological detail: while an Artin braid constructed by circling punctures on a plane is non-trivial, its spherical counterpart-represented by the sequence [latex]b_1b_2b_1b_2b_1[/latex]-collapses to a topologically trivial loop when all but one puncture remain fixed.](https://arxiv.org/html/2602.18748v1/graphics/SphericalBraid-labeled.png)
A new theoretical model details how superconducting islands can induce and stabilize non-abelian anyons within two-dimensional fractional quantum Hall liquids.
Seeing Symmetry: A New Way to Analyze Materials with Light
Researchers have developed a novel Raman spectroscopy technique that unlocks hidden details about a material’s crystalline structure with unprecedented sensitivity.
The High-Energy Frontier: Unveiling the Limits of Particle Scattering
![The study demonstrates how fitting parameters - [latex]\sigma_{t+} [/latex], [latex]\sigma_{t-} [/latex], [latex]\rho_{+} [/latex], and [latex]\rho_{-} [/latex] - using equations derived from data at varying minimum transverse momentum scales ([latex]s_{min} [/latex] of 5 GeV, 30 GeV, and 1 TeV) reveals dependencies inherent within the DB24 dataset, where fitted values incorporate a specific data subset while additional points serve for validation.](https://arxiv.org/html/2602.20005v1/x1.png)
A new analysis of proton-proton and proton-antiproton collisions suggests we may be approaching fundamental limits on how particles interact at ever-increasing energies.
Beyond the Horizon: Can Spinning Gyroscopes Reveal Naked Singularities?
![Within the ergoregion of a rotating Kerr-Newman black hole, orbital velocity Ω diverges near the central region for naked singularities, distinctly differentiating their behavior from that of a black hole where Ω remains finite, a phenomenon observable across varying [latex] Q [/latex] values and measured in units of [latex] M^{-1} [/latex] as a function of radial coordinate [latex] r [/latex] in units of [latex] M [/latex].](https://arxiv.org/html/2602.18972v1/x6.png)
A new analysis suggests that the precession of test gyroscopes could distinguish between the event horizons of black holes and the potentially observable surfaces of naked singularities.
Decoding Student Drive: How Language Reveals Potential in Quantum Computing
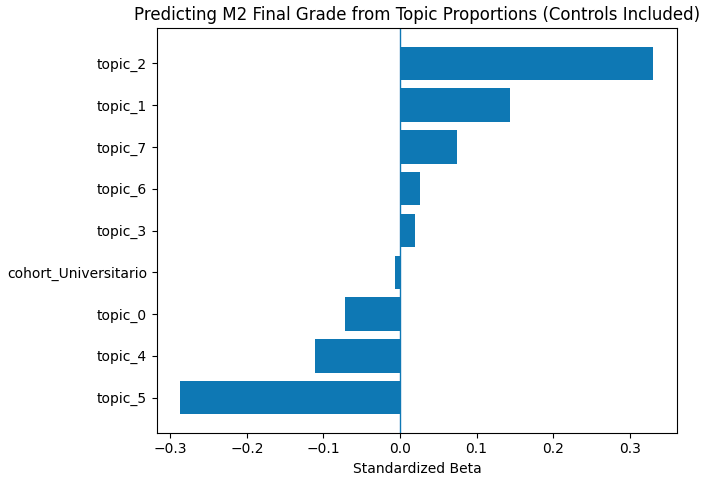
A new study reveals that the language used in short application responses can predict early success in a demanding quantum computing program.
Easing the Cosmic Puzzle: A New Look at Dark Energy
A new analysis suggests quintessence models with exponential potentials can significantly reduce the fine-tuning problem plaguing dark energy explanations.
Relativity and the Shape of Equilibrium
![The thermodynamic curvature of relativistic fermions exhibits a distinct relationship with the chemical potential within a three-dimensional system undergoing an isothermal process [latex] \beta = 1 [/latex], suggesting an inherent sensitivity of fermionic behavior to subtle changes in energetic conditions.](https://arxiv.org/html/2602.19759v1/x4.png)
New research reveals how relativistic effects fundamentally alter the geometric properties of ideal gases, impacting condensation and equilibrium behavior.
Echoes of Creation: How Scalar Fields Warp the Early Universe
A new kinetic theory framework reveals how dynamic scalar fields in K-essence cosmology influence the propagation of photons, potentially leaving subtle imprints on the cosmic microwave background.
Dark Matter’s Fingerprint on Colliding Black Holes
![For parameters E=100, [latex]r_s[/latex]=0.5, and [latex]\rho_s[/latex]=0.2-corresponding to conditions depicted in the lower panel of Figure 1 using metric (19)-gravitational-wave signals exhibit irregular amplitude modulation and a loss of quasi-periodic structure, indicative of the stochastic nature of the orbital dynamics underlying these chaotic regimes.](https://arxiv.org/html/2602.19541v1/x23.png)
New research suggests that the chaotic influence of dark matter halos can leave detectable signatures in the gravitational waves emitted by black hole mergers.