Dancing on the Edge of Chaos: Exploring Herman Rings

Author: Denis Avetisyan

This review delves into the fascinating world of Herman rings, complex dynamical systems exhibiting a delicate balance between order and unpredictability.

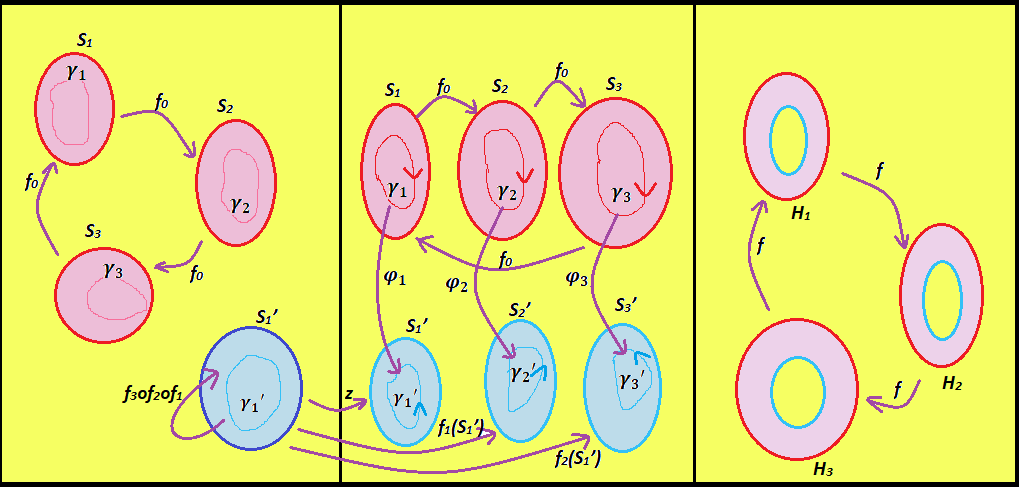
A 33-periodic Herman ring has been constructed, demonstrating a complex, repeating pattern in phase space topology.

A comprehensive survey of the structure, dynamics, and unresolved questions surrounding Herman rings in rational and transcendental meromorphic functions.

Despite significant advances in complex dynamics, the subtle interplay between connectivity and periodicity within Fatou sets remains a challenging area of study. This paper, ‘Herman Rings: Structure, Dynamics, and Open Problems’, provides a comprehensive survey of Herman rings-doubly connected periodic components of the Fatou set-in both rational and transcendental meromorphic maps. We detail established construction techniques, known non-existence results, and critically, highlight the persistent open questions surrounding their prevalence and properties. Given the profound impact these rings have on a function’s global dynamics, what further insights will unlock a complete understanding of their role in complex systems?

Unveiling Order Within Complexity: Beyond Rationality

Many conventional mathematical models are built upon rational functions – expressions defined as the ratio of two polynomials. While effective in certain scenarios, these functions often oversimplify the inherent intricacies of complex systems. This simplification stems from an assumption of predictable, linear behavior, which rarely holds true in the natural world. Phenomena like turbulence in fluids, population dynamics, or even the spread of disease exhibit non-linear interactions and feedback loops that rational functions struggle to accurately represent. Consequently, predictions based solely on these models can diverge significantly from observed reality, particularly when dealing with iterative processes or sensitive dependence on initial conditions. A more nuanced approach, incorporating tools that account for non-linearity and feedback, is therefore essential for a complete understanding of these systems and their unpredictable behaviors.

Iterated functions, those where the output of one calculation becomes the input for the next, frequently reveal behaviors far removed from their initial simplicity. While a function might appear straightforward, repeated application can generate astonishingly complex patterns, even from remarkably simple starting values. This isn’t merely a mathematical curiosity; these systems can exhibit sensitive dependence on initial conditions – often referred to as the “butterfly effect” – where tiny alterations in the starting point lead to drastically different outcomes. Furthermore, they can produce cycles, chaotic behavior, and even fractal patterns, defying intuitive predictions and demonstrating that seemingly deterministic systems are not always predictable. The study of these dynamics requires moving beyond linear approximations and embracing tools from chaos theory and nonlinear dynamics to truly understand the underlying mechanisms at play, revealing a universe of hidden complexity within even the most basic equations.

The accurate depiction of real-world phenomena-from the swirling patterns of fluid flow to the intricate processes within biological systems-often necessitates moving beyond the limitations of traditional rational models. These systems aren’t governed by simple, predictable equations; instead, they exhibit complex dynamics arising from feedback loops and nonlinear interactions. Consequently, researchers are increasingly turning to tools like chaos theory and dynamical systems analysis to understand behaviors that appear random or unpredictable. These approaches allow for the modeling of emergent properties and sensitive dependence on initial conditions, offering insights that linear approximations simply cannot provide. Successfully capturing these intricacies is not merely an academic exercise; it has profound implications for fields like meteorology, ecology, and medicine, allowing for more accurate predictions and potentially, greater control over complex processes.

Mapping Stability: Exploring the Fatou Set

The Fatou set, in the context of iterating complex functions, is defined as the set of points for which nearby iterations remain bounded; that is, the sequence of iterates $f^n(z)$ does not diverge to infinity. Formally, a point $z_0$ belongs to the Fatou set if there exists a neighborhood $U$ of $z_0$ such that the orbit of every point in $U$ under iteration of the function $f$ is bounded. This characteristic allows for local analysis and the application of techniques like linearization and normal forms, providing a crucial starting point for understanding the global dynamics of the function despite the often chaotic behavior exhibited elsewhere. The complement of the Fatou set is known as the Julia set, representing points where this bounded behavior fails, and is typically more complex.

Siegel disks are connected components within the Fatou set characterized by quasi-periodic dynamics; specifically, iterates of a function restricted to a Siegel disk rotate points around the disk’s center by an irrational angle. This contrasts with periodic points which return to their starting location after a finite number of iterations, or rationally periodic points which exhibit rotational symmetry after a finite number of iterations. The irrationality of the rotation angle prevents the iterates from ever exactly repeating their positions, resulting in a dense orbit that fills an annular region. While not chaotic, the behavior is not simply predictable, exhibiting a complex interplay between order-the confinement within the disk-and complexity arising from the non-repeating nature of the rotation. $f(z) = e^{i\alpha}z$ represents a simple rotation where α is an irrational number, often used to model dynamics within a Siegel disk.

Analysis within multiply connected regions of the Fatou set presents significant challenges due to the failure of standard analytic techniques like conformal mapping and the argument principle. These regions, topologically distinct from simply connected domains, necessitate the application of more advanced tools such as Riemann surfaces and branched covering theory to accurately characterize their dynamics. The presence of nontrivial fundamental groups and associated monodromy complicates the determination of stable manifolds and the overall behavior of iterated functions within these domains. Consequently, investigations frequently rely on numerical methods and computational techniques to approximate solutions and gain insight into the complex dynamics occurring in multiply connected components of the Fatou set.

The Herman ring, visualized for <span class="katex-eq" data-katex-display="false">\alpha = 1.9</span> and <span class="katex-eq" data-katex-display="false">\beta = 0.5</span>, is bounded by the blue and red curves representing the orbits of the free critical points <span class="katex-eq" data-katex-display="false">\frac{-1 \pm \sqrt{1 - \beta^2}}{\beta}</span>. — The Herman ring, visualized for $\alpha = 1.9$ and $\beta = 0.5$ , is bounded by the blue and red curves representing the orbits of the free critical points $\frac{-1 \pm \sqrt{1 - \beta^2}}{\beta}$ .

Sculpting Dynamics: Conformal Mapping and Teichmüller Theory

Conformal mapping is a transformation of complex functions that locally preserves angles and shapes, meaning infinitesimal geometric figures are preserved during the transformation. Mathematically, a function $f: U \rightarrow V$ between two domains $U$ and $V$ in the complex plane is conformal if it is analytic and its derivative $f'(z)$ is non-zero for all $z$ in $U$ . This preservation of angles is crucial in various applications, including fluid dynamics, electrostatics, and complex analysis, as it simplifies the analysis of geometric problems by allowing transformations to be performed without distorting the local geometric relationships. While lengths are not necessarily preserved, the preservation of angles allows for the mapping of complex domains onto simpler ones, facilitating analysis and solution finding.

Teichmüller theory provides a rigorous mathematical framework for analyzing the space of all possible deformations of a complex function that preserve its conformal structure. This space, known as Teichmüller space, is equipped with a natural metric-the Teichmüller metric-allowing for quantifiable measurements of how different deformations relate to one another. Crucially, this framework enables the precise control of a function’s dynamical behavior by characterizing how small changes in the conformal structure-such as stretching or shearing-affect the function’s iterations and stability. By studying the geometry of Teichmüller space, researchers can determine which deformations lead to specific dynamical properties, such as the creation or annihilation of periodic orbits, or the control of chaotic behavior. The theory relies on the concept of Beltrami coefficients to parameterize these deformations and ensures that the resulting functions remain within a defined equivalence class, preserving key topological features.

Quasiconformal surgery is a technique used in complex dynamics to modify a function’s behavior by making localized, geometrically controlled changes. This involves excising a domain from the function and replacing it with a quasiconformal map – a mapping that locally behaves like a conformal map but allows for a limited degree of distortion. By strategically applying quasiconformal surgeries, researchers can precisely control the function’s dynamics, such as creating or eliminating periodic orbits, or altering the stability of fixed points. The combination of conformal mapping and Teichmüller theory provides the necessary framework for analyzing and constructing these surgeries, enabling the creation of functions with predetermined dynamical characteristics, even in highly complex systems where direct construction would be intractable. This allows for rigorous study of complex dynamics through controlled manipulation and analysis of function behavior.

The Threshold of Predictability: The Brjuno Number and Quasi-Periodic Regularity

The behavior of quasi-periodic dynamical systems – those exhibiting complex, non-repeating patterns – hinges critically on a value known as the Brjuno number. This number acts as a decisive threshold, effectively partitioning these systems into realms of predictable and chaotic behavior. Systems with a Brjuno number sufficiently small demonstrate a remarkable degree of regularity; orbits remain confined and predictable over extended timescales. Conversely, when the Brjuno number exceeds a certain limit, the dynamics rapidly descend into chaos, with trajectories becoming highly sensitive to initial conditions and long-term prediction becoming impossible. This seemingly abstract mathematical condition has profound implications, as it dictates whether a system will exhibit stable, understandable behavior or succumb to the unpredictable fluctuations characteristic of chaos, a principle relevant to fields ranging from celestial mechanics to the study of fluid turbulence.

The regularity of quasi-periodic dynamics hinges on a detailed examination of a function’s trajectory – both forward and backward – and, crucially, how these orbits approach the function’s ‘omitted’ values – those points the function never reaches. By analyzing how quickly these orbits ‘escape’ or converge towards these omissions, mathematicians can gauge the system’s long-term predictability. An orbit exhibiting ‘escape’ – where orbits diverge rapidly – indicates chaotic behavior, while a controlled approach towards omitted values suggests a degree of regularity. This interplay between forward and backward dynamics isn’t simply about where a function goes, but how it gets there, and the subtle dance around these inaccessible points is the key to unlocking the underlying order – or disorder – of seemingly complex systems. The rate of this convergence, quantified through mathematical tools, ultimately determines whether a system will remain bounded and predictable over extended timescales.

The principles governing quasi-periodic dynamics, as illuminated by the Brjuno number, extend far beyond the realm of pure mathematics, offering powerful tools for analyzing stability in a surprisingly broad spectrum of scientific fields. From celestial mechanics – predicting the long-term behavior of planetary orbits and asteroids – to the study of particle accelerators, where maintaining beam stability is paramount, these insights prove invaluable. Furthermore, the understanding of regularity derived from this work informs models in climate science, helping to assess the predictability of long-term weather patterns, and even impacts financial modeling, where identifying persistent, non-chaotic behaviors is crucial for risk assessment. Ultimately, the ability to discern order within seemingly complex systems, established through this mathematical framework, provides a foundation for improved prediction and control across diverse scientific and engineering disciplines.

The Herman ring, a yellow region bounded by the orbits of the critical points <span class="katex-eq" data-katex-display="false">\frac{19+\sqrt{105}}{16}</span> (blue) and <span class="katex-eq" data-katex-display="false">\frac{19-\sqrt{105}}{16}</span> (red), contains invariant Jordan curves (black) for the function <span class="katex-eq" data-katex-display="false">e^{2\pi i\frac{\sqrt{5}-1}{2}}\frac{z^{2}(z-4)}{1-4z}</span>. — The Herman ring, a yellow region bounded by the orbits of the critical points $\frac{19+\sqrt{105}}{16}$ (blue) and $\frac{19-\sqrt{105}}{16}$ (red), contains invariant Jordan curves (black) for the function $e^{2\pi i\frac{\sqrt{5}-1}{2}}\frac{z^{2}(z-4)}{1-4z}$ .

Beyond the Ring: Shaping the Future of Dynamical Systems

The Herman ring stands as a remarkable example of order emerging from apparent complexity within dynamical systems. This structure, a doubly connected component of the Fatou set, isn’t simply periodic-it exhibits a nuanced, quasi-periodic behavior. Unlike a perfectly repeating orbit, trajectories within a Herman ring wind around the central hole in a way that never quite repeats exactly, yet remains confined and stable over vast timescales. This delicate balance, arising from specific irrational relationships between rotation numbers, demonstrates that complex dynamics don’t necessarily equate to chaos; instead, they can manifest as highly structured and predictable patterns. The existence of Herman rings reveals a hidden layer of organization within seemingly erratic systems, suggesting that stability and complexity can coexist in unexpected ways, and offering a powerful model for understanding similar phenomena across various scientific disciplines.

The significance of the Herman ring extends beyond its mathematical elegance, offering a foundational framework for engineering complex dynamical systems. Researchers are actively adapting the analytical tools – stemming from the detailed understanding of the ring’s intricate, yet stable, structure – to control behaviors in fields ranging from accelerator physics and plasma confinement to the design of secure communication networks and even the optimization of robotic locomotion. This blueprint allows for the creation of systems exhibiting quasi-periodic motion, avoiding the chaotic unpredictability often associated with complex dynamics while still achieving a high degree of flexibility and responsiveness. The ability to reliably sculpt these dynamics represents a substantial advancement, promising innovations in technologies reliant on precise, controlled movement and signal processing.

This research presents a thorough survey of the current understanding of Herman rings, intricate structures arising in the study of dynamical systems. The paper consolidates existing knowledge regarding their fundamental properties – including their role as doubly connected periodic Fatou components exhibiting remarkably stable, quasi-periodic behavior – and details the various mathematical techniques employed in their construction. Beyond a comprehensive overview of established results, the study also highlights several persistent open questions and potential avenues for future investigation, serving as a valuable resource for researchers seeking to further explore these fascinating and complex dynamical objects. It aims to provide a unified perspective on the field, charting both progress and the remaining challenges in understanding these unique components of dynamical systems.

The Poincaré surface of section reveals a cycle of 33-periodic Herman rings, indicating quasi-periodic motion.

The exploration of Herman rings, as detailed in the study of transcendental meromorphic maps, reveals a fascinating interplay between structure and dynamics. These doubly connected components, residing within the Fatou set, necessitate a rigorous examination of their properties to discern their existence and behavior. This pursuit echoes Stephen Hawking’s sentiment: “Intelligence is the ability to adapt to any environment.” Just as intelligence requires adaptation, understanding these complex systems demands a flexible approach, employing techniques like quasiconformal surgery to probe the boundaries of established knowledge and formulate new hypotheses about the Julia set and rational maps. The study demonstrates that each visual detail-a connection, a boundary, a singularity-offers an opportunity to test a hypothesis and expand model understanding.

Where Do the Rings Lead?

The persistent allure of Herman rings lies not in their construction-though that remains a nontrivial exercise-but in their frustrating resistance to complete categorization. The study reveals, with characteristic irony, that understanding these simply connected components demands a grasp of the broader, infinitely more complex dynamics of rational and transcendental maps. Each proven non-existence result, each successful construction, serves less as a full stop and more as a precise delineation of the unknown. The boundary between provable and unprovable, between existence and non-existence, appears less a sharp line and more a fractal coastline.

Future progress likely hinges on bridging the techniques of quasiconformal surgery with a deeper understanding of the parameter space of these functions. While the rigidity results offer tantalizing glimpses of order, the sheer diversity of potential behaviors suggests that a unified theory remains distant. The challenge isn’t merely to find more rings, but to discern the underlying principles governing their distribution and stability-to move beyond cataloging instances toward understanding the landscape itself.

Ultimately, the quest for a complete understanding of Herman rings serves as a potent reminder: every image is a challenge to understanding, not just a model input. The rings aren’t the destination, but a particularly elegant set of signposts pointing towards the deeper mysteries of complex dynamics.

Original article: https://arxiv.org/pdf/2512.24118.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/