Simulating the Quantum Vacuum in Curved Space

Author: Denis Avetisyan

New computational methods are opening a window into the exotic particle creation predicted by quantum field theory in the presence of strong gravitational effects.

The emergence of fermion-antifermion pairs, quantified by number density and momentum spectrum at times <span class="katex-eq" data-katex-display="false">\tau = 0.1\,\lambda</span>, <span class="katex-eq" data-katex-display="false">\tau = 1.3\,\lambda</span>, and <span class="katex-eq" data-katex-display="false">\tau = 10\,\lambda</span>, correlates with spacetime curvature-specifically, the Ricci scalar <span class="katex-eq" data-katex-display="false">R(\xi)</span>-calculated from equations governing a system discretized across <span class="katex-eq" data-katex-display="false">N = 2^{11}</span> lattice sites with a time step of <span class="katex-eq" data-katex-display="false">\delta\tau = 0.01\,\lambda</span>, suggesting that particle creation is intrinsically linked to the geometry of spacetime itself. — The emergence of fermion-antifermion pairs, quantified by number density and momentum spectrum at times $\tau = 0.1\,\lambda$ , $\tau = 1.3\,\lambda$ , and $\tau = 10\,\lambda$ , correlates with spacetime curvature-specifically, the Ricci scalar $R(\xi)$ -calculated from equations governing a system discretized across $N = 2^{11}$ lattice sites with a time step of $\delta\tau = 0.01\,\lambda$ , suggesting that particle creation is intrinsically linked to the geometry of spacetime itself.

This work presents a numerical framework for studying fermion pair creation in two-dimensional curved spacetimes using Computational Quantum Field Theory and the split-operator method.

The conventional understanding of vacuum stability is challenged by the prediction of particle creation in dynamic gravitational fields, analogous to the Schwinger effect. This work, ‘Computational quantum field theory for fermion pair creation in 2-dimensional curved spacetimes’, introduces a numerical framework extending Computational Quantum Field Theory (CQFT) to investigate fermion pair creation induced by spacetime curvature. By evolving the Dirac equation in a $1+1$ -dimensional curved spacetime with a localized Gaussian deformation, we demonstrate a method for quantifying vacuum excitation and its dependence on curvature strength. Will this approach pave the way for modeling particle creation in more complex, time-dependent scenarios incorporating both gravity and electromagnetism?

The Emergence of Reality: Curvature and the Quantum Vacuum

The accurate depiction of particle creation fundamentally demands a departure from the simplifying assumptions of flat spacetime. While flat spacetime models serve as useful approximations in many scenarios, they break down when gravitational fields become sufficiently strong, such as near black holes or during the early universe. In these regimes, spacetime curvature dramatically influences particle behavior and, crucially, enables the spontaneous creation of particle-antiparticle pairs from the vacuum. This process isn’t merely a theoretical curiosity; it’s predicted by quantum field theory in curved spacetime and has implications for understanding phenomena like Hawking radiation and the cosmological constant. Therefore, a robust theoretical framework capable of describing spacetime as a dynamic, curved entity-rather than a static, flat background-is essential for modeling these processes and accurately predicting the evolution of the universe.

A fundamental challenge in describing physical phenomena within curved spacetime lies in bridging the gap between the familiar, flat-space physics of special relativity and the complexities of general relativity. The tetrad formalism elegantly addresses this by introducing a set of four vector fields – the tetrads – which define local Lorentz frames at each point in the curved spacetime. These frames serve as a local ‘flat’ approximation, allowing physicists to apply the well-established principles of special relativity within a small region. Crucially, the tetrads provide the necessary transformation rules to convert between the coordinates of these local frames and the global, curved spacetime coordinates. This capability is essential for accurately calculating physical quantities, such as particle trajectories and energy densities, because it ensures that physical laws are expressed in a coordinate-independent manner. Without this precise connection, calculations in curved spacetime would be riddled with inaccuracies and inconsistencies, hindering a proper understanding of gravitational phenomena.

Accurately describing the behavior of spin-1/2 particles-like electrons-within the warped geometry of curved spacetime demands a nuanced approach to the Dirac equation. Unlike flat spacetime, where particle transformations are straightforward, curved spacetime necessitates the inclusion of the spin connection, a mathematical object representing the effect of curvature on a particle’s intrinsic angular momentum, or spin. This spin connection appears within the covariant derivative, which replaces the standard partial derivative to ensure the Dirac equation remains mathematically consistent and physically meaningful as it describes spinor transformations. Failing to account for these effects leads to unphysical predictions; therefore, the proper formulation using the covariant derivative and spin connection is essential for predicting particle behavior in strong gravitational fields and understanding phenomena like Hawking radiation and the dynamics of black holes. The resulting equation, incorporating these corrections, allows physicists to model how a particle’s spin precesses due to the curvature of spacetime, providing a crucial link between quantum mechanics and general relativity.

The number of created fermion-antifermion pairs increases with time and saturates at higher values for wider Gaussian curvatures <span class="katex-eq" data-katex-display="false">r_0 = 1\lambda</span>, <span class="katex-eq" data-katex-display="false">r_0 = \sqrt{2}\lambda</span>, and <span class="katex-eq" data-katex-display="false">r_0 = \sqrt{3}\lambda</span> on a <span class="katex-eq" data-katex-display="false">100\lambda</span> lattice with <span class="katex-eq" data-katex-display="false">N = 2^{11}</span> sites. — The number of created fermion-antifermion pairs increases with time and saturates at higher values for wider Gaussian curvatures $r_0 = 1\lambda$ , $r_0 = \sqrt{2}\lambda$ , and $r_0 = \sqrt{3}\lambda$ on a $100\lambda$ lattice with $N = 2^{11}$ sites.

Simplifying the Complex: A Pathway Through Curvature

A Gaussian deformation of flat spacetime provides a mathematically accessible model for studying the effects of gravitational curvature. This approach involves introducing a spatially varying scale factor to the flat Minkowski metric, resulting in a perturbed spacetime that retains analytical tractability while incorporating curvature. Specifically, the metric is deformed such that the resulting curvature tensor, while non-zero, is controlled by the parameters defining the Gaussian profile. This allows researchers to systematically investigate how quantum fields propagate and interact in the presence of curvature, providing insights into phenomena relevant to cosmology and black hole physics without the full complexity of general relativistic spacetimes. The resulting simplified geometry facilitates both analytical calculations and numerical simulations, enabling controlled tests of theoretical predictions.

Conformal flatness, a technique for simplifying the analysis of curved spacetime, is achieved through the implementation of null coordinates. This transformation allows for the metric tensor to be expressed in a form where the spatial components are functions solely of a single coordinate, effectively “flattening” the spatial geometry while preserving the causal structure. By exploiting this property, calculations involving the wave equation and field propagators become significantly more tractable, reducing the computational cost associated with simulating quantum fields in curved spacetime. The simplification stems from the ability to perform many calculations as if they were occurring in flat spacetime, with corrections applied to account for the residual curvature effects, leading to substantial efficiency gains in numerical simulations.

Computational Quantum Field Theory (CQFT) facilitates real-time simulations within curved spacetime frameworks by adapting established quantum field theory techniques. Recent implementations have demonstrated convergence with a spatial lattice resolution of $\Delta \xi = 0.0488\lambda$ and a corresponding time step of $\Delta \tau = 0.01\lambda$ . These parameters define the granularity of the spacetime discretization used in the numerical solution, and their values represent a validated balance between computational cost and simulation accuracy for the given model.

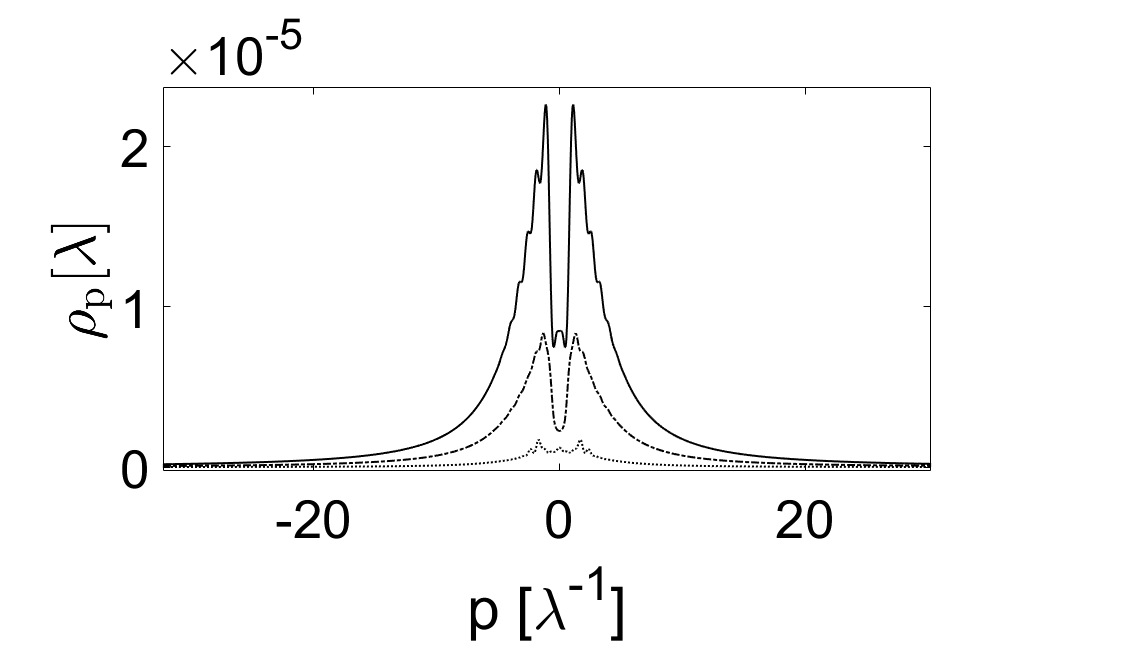
The spectrum of created fermion-antifermion pairs increases with Gaussian curvature strength until saturation, with higher values of β (0.8 vs. 0.5) indicating a broader range of created modes.

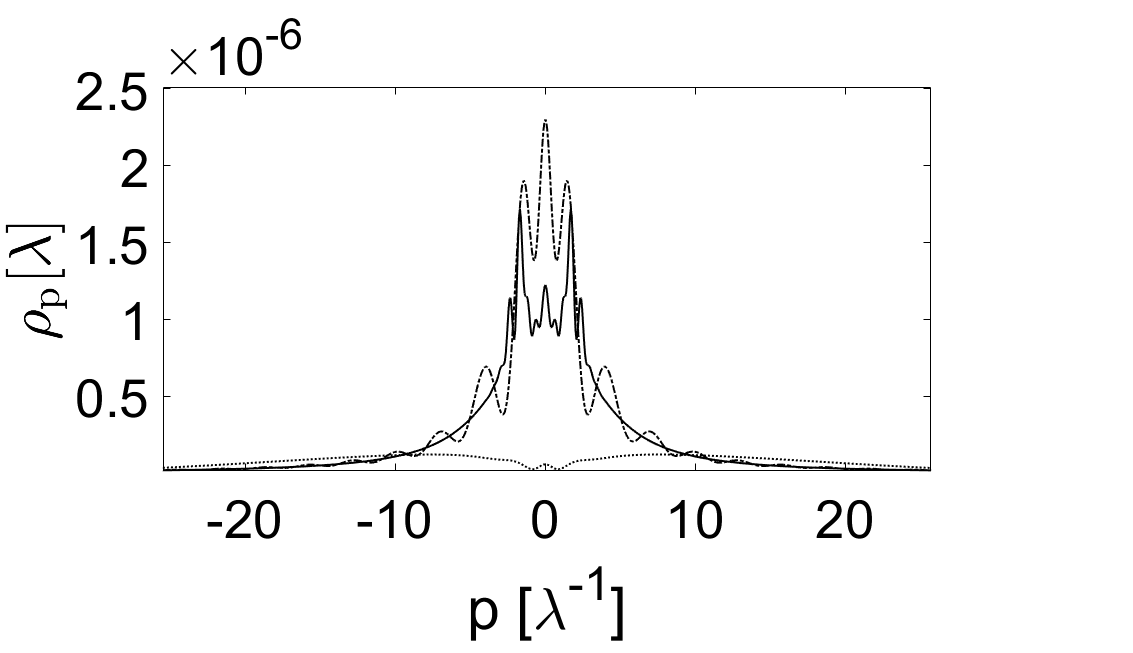
Witnessing Emergence: The Vacuum in a Curved Universe

The research demonstrates that spacetime curvature directly induces the excitation of the quantum vacuum state. This excitation manifests as the creation of particle-antiparticle pairs, effectively converting gravitational potential energy into observable matter. The process isn’t a spontaneous fluctuation, but a direct consequence of the curvature’s influence on the vacuum’s energy density, leading to a measurable increase in particle number. This observed pair creation provides evidence supporting the theoretical prediction that strong gravitational fields can act as a source for particle production, challenging the classical notion of a truly empty vacuum.

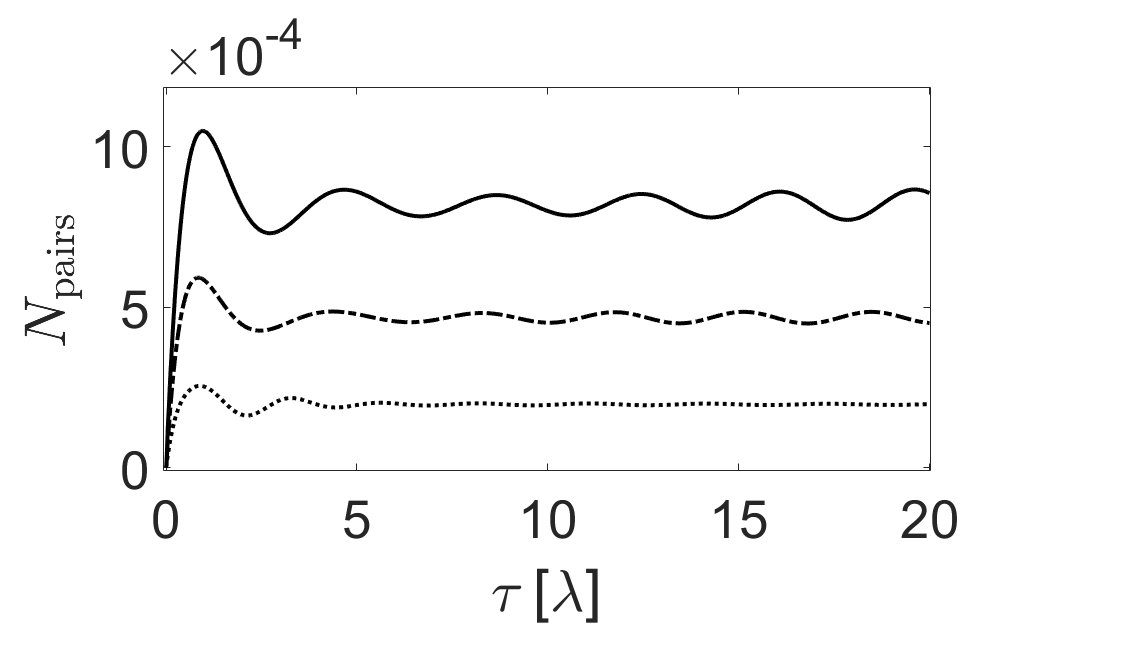
The simulation of real-time quantum field dynamics necessitates the calculation of the time evolution operator $U(t) = \exp(-iHt)$ , where H is the Hamiltonian. Direct computation of this operator is generally intractable; therefore, a split-operator method was implemented to efficiently approximate it. This technique decomposes the time evolution into a series of smaller, more manageable steps, each involving the exponential of a simpler operator. Specifically, the time evolution operator is approximated as a product of two exponentials: $U(t) \approx \exp(-i\frac{t}{2}H_1)\exp(-i\frac{t}{2}H_2)$ . This decomposition allows for the accurate calculation of the time evolution with reduced computational cost, enabling the simulation of vacuum dynamics and subsequent pair creation over extended time scales.

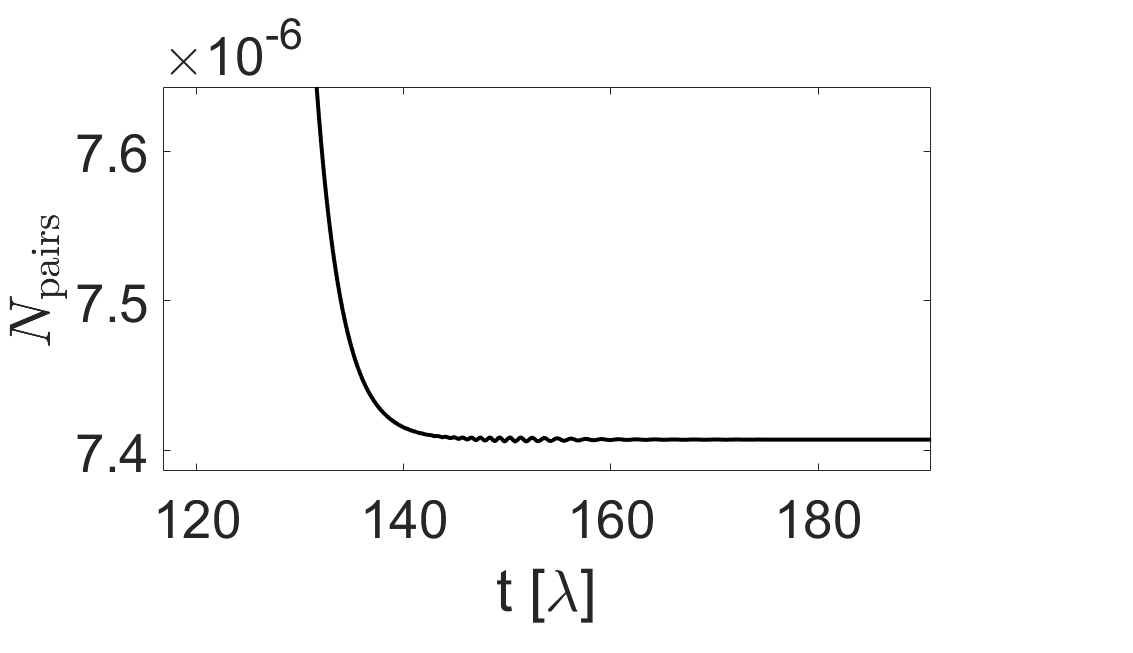
The simulation accurately models the creation of particle-antiparticle pairs from the vacuum state induced by spacetime curvature. This is achieved through a precise time evolution operator, validated by a demonstrated norm preservation of $3.4 \times 10^{-{13}}$ over a simulation duration of 20λ. This high degree of accuracy confirms the model’s ability to reliably simulate the real-time dynamics of pair creation, indicating that spacetime curvature can indeed lead to observable particle production as predicted by theoretical frameworks.

Simulations using CQFT show that a Sauter step with <span class="katex-eq" data-katex-display="false">E_0 = 1/4</span> and <span class="katex-eq" data-katex-display="false">\omega = 0.1</span> results in the creation of approximately <span class="katex-eq" data-katex-display="false">7.4 \\times 10^{-6}</span> fermion-antifermion pairs, a value consistent with adiabatic particle number calculations and verified through lattice refinement. — Simulations using CQFT show that a Sauter step with $E_0 = 1/4$ and $\omega = 0.1$ results in the creation of approximately $7.4 \\times 10^{-6}$ fermion-antifermion pairs, a value consistent with adiabatic particle number calculations and verified through lattice refinement.

Beyond the Model: Implications and Future Trajectories

The findings of this study establish a key framework for interpreting particle generation within the extreme gravitational environments found in astrophysical phenomena. Regions around black holes, neutron stars, and in the nascent universe all feature intense gravity that significantly impacts quantum field behavior. This research demonstrates a method to model particle creation – not as arising from a void, but as a consequence of the spacetime curvature itself. By accurately predicting particle production rates in these strong-field regimes, it provides essential tools for analyzing observational data and testing theoretical predictions regarding the dynamics of these cosmic objects and the fundamental interplay between gravity and quantum mechanics. This foundational understanding is crucial for progressing towards a more complete picture of the universe’s most energetic and mysterious processes.

The analytical techniques developed in this study are not limited to the simplified spacetime geometries initially explored; they offer a pathway to investigate far more complex astrophysical scenarios. Researchers can now extend these methods to model particle creation in environments with dynamic or non-uniform gravitational fields, moving beyond static, spherically symmetric backgrounds. This capability is particularly crucial for understanding the interplay between gravity and quantum fields in extreme conditions, such as those near black holes or during the very early universe. By refining these approaches, scientists aim to probe the fundamental limits of current theoretical frameworks and potentially uncover novel phenomena arising from the intersection of general relativity and quantum field theory, offering deeper insights into the nature of spacetime and the origins of the cosmos.

The established computational framework offers a promising avenue for investigating some of the most enigmatic phenomena in the universe. Specifically, researchers can now apply these techniques to model Hawking radiation, the theoretical emission of particles from black holes, and gain deeper insights into the quantum effects of strong gravitational fields. Furthermore, extending the simulations to the conditions of the very early universe – a period of extreme density and curvature – may reveal crucial information about the origins of cosmic structure and the fundamental laws governing spacetime. These investigations promise to move beyond purely theoretical considerations, providing a means to test predictions about quantum gravity and ultimately refine our understanding of the cosmos’ evolution and its ultimate fate.

The study demonstrates a shift from seeking overarching control in theoretical frameworks to embracing localized numerical solutions within complex spacetimes. Much like a biological system adapting to its environment, the split-operator method allows for the emergence of solutions-fermion pair creation-from the interplay of local quantum fluctuations. This mirrors a principle of distributed order, where vacuum excitation isn’t dictated by a central equation but arises from the dynamic interactions within the curved spacetime itself. As Mary Wollstonecraft observed, “The mind, when once awakened, will never rest until it has satisfied its curiosity.” This computational approach, allowing exploration of previously inaccessible regimes, embodies that relentless pursuit of understanding, finding order not through imposed structure but through revealing the inherent dynamics of the quantum vacuum.

Where Do We Go From Here?

The extension of Computational Quantum Field Theory to curved spacetimes, as demonstrated, offers a valuable, if computationally intensive, means of examining fermion pair creation. It’s tempting to speak of ‘modeling’ Hawking radiation, but such language implies a degree of control that is, at best, illusory. Global regularities emerge from simple rules – the Dirac equation, the split-operator method – and any attempt at directive management of quantum vacuum excitation will likely introduce artifacts. The true utility lies in allowing the system to reveal its behavior, rather than attempting to impose one.

Current limitations are self-evident. Computational cost restricts simulations to relatively small spacetimes and short timescales. A key avenue for progress lies not in brute-force computation, but in developing more efficient algorithms and exploiting inherent symmetries. Furthermore, this work primarily addresses idealized scenarios. The next step involves incorporating more realistic spacetime geometries – those encountered near rotating black holes, or in cosmological settings – and investigating the impact of backreaction on the curved background itself.

Ultimately, the goal isn’t to reproduce observed phenomena – that is merely a validation of the underlying formalism. It is to explore the emergent behavior of quantum fields in extreme conditions, and to refine the understanding of how local interactions give rise to the large-scale structures observed in the universe. The universe doesn’t need an architect; it simply is.

Original article: https://arxiv.org/pdf/2602.07330.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Emergence of Reality: Curvature and the Quantum Vacuum

Simplifying the Complex: A Pathway Through Curvature

Witnessing Emergence: The Vacuum in a Curved Universe

Beyond the Model: Implications and Future Trajectories

Where Do We Go From Here?

See also: