Author: Denis Avetisyan
New research explores how fundamental quantum uncertainty principles are affected by the extreme gravity of Schwarzschild black holes, revealing a link between spacetime and quantum coherence.
This study derives a generalized entropic uncertainty relation and investigates quantum entanglement and coherence in the vicinity of a Schwarzschild black hole using Kruskal coordinates.
The fundamental tenets of quantum mechanics, particularly the uncertainty principle, present a persistent challenge when applied to extreme gravitational environments. This is explored in ‘Generalized entropic uncertainty relation and non-classicality in Schwarzschild black hole’, which introduces a refined entropic uncertainty relation and investigates its implications for quantum coherence and entanglement near black holes. The study demonstrates a tighter bound on uncertainty and reveals a direct equivalence between entanglement and l_1-norm coherence for multi-partite systems, alongside a quantifiable degradation of quantum resources with increasing Hawking temperature. How might these findings reshape our understanding of the interplay between quantum information and the event horizon of a black hole?
The Void Isn’t Empty: Quantum Fluctuations Around Black Holes
The very notion of “empty” space, typically described as the quantum vacuum, undergoes a dramatic transformation when considered within the intensely warped spacetime surrounding a black hole. Unlike the flat, uniform vacuum of conventional quantum field theory, the vacuum near a black hole becomes a dynamic, observer-dependent state. This isn’t merely a theoretical curiosity; the curvature of spacetime itself introduces an energy density, effectively turning the vacuum into a sea of virtual particles constantly popping into and out of existence. These particles aren’t simply a mathematical artifact; their behavior is intricately linked to the black hole’s gravitational field and, crucially, appears different to observers in different reference frames. The standard definition of a vacuum – the lowest energy state – breaks down, giving rise to multiple, equally valid descriptions of what constitutes “nothing” near a black hole, a key ingredient in the enduring black hole information paradox and a fundamental challenge to reconciling quantum mechanics with general relativity.
The very notion of ‘empty’ space, or the vacuum, fractures when considered near a black hole, manifesting as differing perceptions for different observers. One observer, far from the event horizon, perceives the vacuum as being in its ‘Hartle-Hawking’ state – filled with a thermal bath of particles constantly being created and destroyed. However, an observer accelerating into the black hole experiences the ‘Boulware’ vacuum, where particles are absent and the field behaves classically. This fundamental disagreement isn’t a matter of measurement error, but a consequence of the intensely curved spacetime warping the quantum fabric itself. The paradox arises because quantum mechanics dictates information cannot be destroyed, yet if an object falls into a black hole and the Boulware observer sees nothing enter, it appears the object’s information has vanished – a direct conflict with established physical laws and a central challenge in unifying quantum mechanics with general relativity.
Resolving the discrepancies in vacuum state perception near black holes demands a sophisticated mathematical toolkit for characterizing quantum entanglement and coherence. Traditional measures, adequate in flat spacetime, falter when confronted with the intense gravitational gradients and event horizons. Researchers are developing novel techniques – leveraging concepts from quantum information theory and utilizing tools like ρ_A = Tr_B(ρ_{AB}) to describe reduced density matrices – to quantify how strongly quantum states are correlated across vast distances, even when separated by event horizons. These frameworks aim to move beyond simply detecting entanglement to precisely measuring its strength and characterizing its resilience against the disruptive effects of extreme curvature. The ultimate goal is to establish a quantifiable link between quantum correlations and the preservation of information, potentially revealing how information seemingly lost within a black hole might actually be encoded in subtle correlations within the Hawking radiation or remain accessible through wormhole-like connections – a key step towards resolving the black hole information paradox.
Density Matrices: Describing What We Don’t Know
Unlike the wave function, which fully describes a pure quantum state, many physical systems exist as statistical mixtures of states. The density matrix, denoted as ρ, provides a complete description of both pure and mixed quantum states. For a pure state | \psi \rangle , the density matrix is defined as \rho = | \psi \rangle \langle \psi | . However, for a mixed state, which is a probabilistic ensemble of pure states | \psi_i \rangle occurring with probabilities p_i , the density matrix is calculated as \rho = \sum_i p_i | \psi_i \rangle \langle \psi_i | . This formalism allows for the treatment of systems where complete knowledge of the state is unavailable, providing a generalized framework for quantum mechanical descriptions.
Quantum coherence, fundamentally linked to the superposition principle, is represented in the density matrix formalism by non-zero off-diagonal elements. These elements describe the quantum correlations between different basis states of the system. In the context of quantum information processing, coherence enables phenomena like quantum interference and entanglement, which are essential resources for algorithms exceeding classical capabilities. Specifically, the degree of coherence dictates the potential for a quantum state to exhibit these properties; a state with high coherence is more susceptible to interference and can maintain entanglement more effectively. Loss of coherence, known as decoherence, degrades these quantum properties and limits the performance of quantum technologies, making the preservation and quantification of coherence a central challenge in the field.
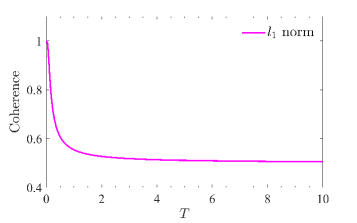
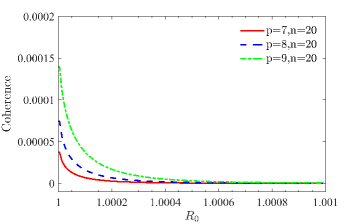
The l1-norm of coherence provides a quantifiable metric for the degree of quantum coherence present in a given quantum state. Calculated as the sum of the absolute values of the off-diagonal elements in the density matrix, this norm allows for a rigorous, numerical assessment of coherence, independent of specific state properties. Importantly, the l1-norm of coherence has been mathematically proven to be identical to quantum concurrence, a measure of entanglement for two-qubit systems. This equivalence establishes a direct, measurable link between coherence and entanglement, demonstrating that coherence, as quantified by the l1-norm, can serve as a proxy for entanglement in certain contexts, and providing a valuable tool for analyzing and characterizing quantum states.
The Schwarzschild metric, while mathematically defined in standard coordinates, exhibits singularities at the event horizon and at r = 0. To address these coordinate singularities and provide a complete description of the spacetime structure, the Kruskal-Szekeres coordinate system is employed. This system is a maximal analytic extension of Schwarzschild spacetime, revealing regions beyond the event horizon and demonstrating that the singularity at r = 0 is not a true singularity, but rather a boundary between different spacetime regions. Kruskal-Szekeres coordinates achieve this by employing a non-standard coordinate transformation that allows for continued geodesic paths through what would appear as singularities in the standard Schwarzschild coordinates, thus revealing the complete causal structure of the spacetime.
The Dirac field, mathematically represented by the Dirac equation (i\gamma^\mu \partial_\mu - m)\psi = 0 , serves as a foundational model for relativistic quantum fields in curved spacetime. Unlike scalar fields, the Dirac field describes fermions - particles with half-integer spin, such as electrons and quarks - and inherently incorporates spin and anti-particle degrees of freedom. Its use allows for the investigation of how gravitational effects, as defined by the spacetime metric, influence particle creation and annihilation, vacuum polarization, and other quantum phenomena. Analysis of the Dirac field’s behavior in Schwarzschild geometry, for instance, reveals modifications to the particle spectrum and the emergence of bound states near the event horizon, providing insights into Hawking radiation and other black hole effects. The field’s properties are determined by its interaction with the spacetime geometry, which modifies the usual flat-space solutions and introduces new, gravitationally induced effects on quantum behavior.
Curvature of spacetime, as predicted by general relativity, modifies the behavior of quantum entanglement. In flat spacetime, entangled particles exhibit correlations consistent with the Bell inequality; however, in the presence of strong gravitational fields, such as those surrounding black holes, these correlations are altered. Specifically, the geometric distortions introduced by spacetime curvature lead to a squeezing of the quantum state, resulting in violations of the Bell inequality that differ in magnitude and form from those observed in flat spacetime. This alteration arises because the modes of the quantum field that constitute the entangled particles experience different time delays and frequency shifts due to the varying gravitational potential, effectively changing the observed correlations and introducing a dependence on the spacetime geometry. These effects are not merely a change in signal strength, but a fundamental alteration of the quantum state itself, demonstrably impacting the entanglement properties.
Entanglement as a Probe: What Does Spooky Action at a Distance Tell Us?
Greenberger-Horne-Zeilinger (GHZ) and Werner states are prototypical examples of multipartite entanglement utilized to investigate the effects of curved spacetime on quantum correlations. Specifically, these states demonstrate alterations in their correlation properties when subjected to gravitational fields, differing from their behavior in flat spacetime. The GHZ state, a maximally entangled state of three qubits, and the Werner state, characterized by a specific level of mixedness, are chosen due to their distinct entanglement structures and relative ease of analysis. Analysis focuses on how spacetime curvature affects the violation of Bell-type inequalities for these states, providing quantifiable evidence of entanglement degradation or modification due to gravitational influences. These alterations are not simply a reduction in entanglement magnitude, but rather a change in the type of correlation exhibited, revealing a fundamental interplay between quantum entanglement and the geometry of spacetime.
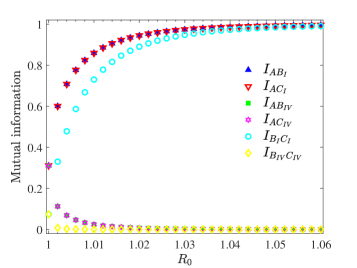
Genuine multipartite concurrence is a quantifiable metric used to assess the entanglement present in systems comprising multiple qubits. Unlike entanglement measures applicable only to two qubits, or those that fail to detect genuine multipartite entanglement (such as biseparable states), genuine multipartite concurrence specifically identifies and quantifies entanglement shared among all qubits in the system. It is calculated based on the reduced density matrices of various subsystems, providing a value between 0 and 1, where 0 indicates no entanglement and 1 represents maximum entanglement. This allows for direct, comparative analysis of entanglement levels across different multipartite quantum states and under varying conditions, such as those induced by curved spacetime or thermal effects, offering a precise tool for investigating the relationship between entanglement and fundamental physics.
Analysis of GHZ and Werner states in curved spacetime demonstrates a quantifiable relationship between spacetime geometry and quantum entanglement. Specifically, alterations in the correlation properties of these multipartite entangled states - measured using genuine multipartite concurrence - indicate a direct influence of the gravitational field on quantum coherence. This influence isn’t merely perturbative; the observed monotonic decrease in coherence with increasing Hawking temperature suggests a fundamental coupling between spacetime curvature and the preservation of quantum information. These findings establish that spacetime geometry actively modifies the shared quantum state, impacting the degree of correlation between constituent qubits and providing a means to probe the structure of spacetime through entanglement measurements.
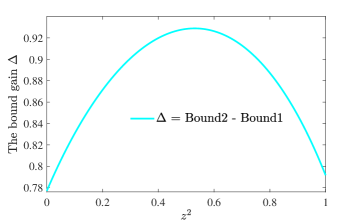
Recent investigations into quantum uncertainty have revealed a deepened understanding of the inherent limits on simultaneously knowing certain properties of a quantum system. The generalized entropic uncertainty relation, a refinement of Heisenberg’s principle, establishes a quantifiable lower bound on the combined uncertainty of non-commuting observables, moving beyond simple variance-based measures to consider information-theoretic constraints. Notably, this relation demonstrates that quantum memory assistance - leveraging prior knowledge stored in an auxiliary system - can reduce this uncertainty, effectively allowing for more precise measurements than previously thought possible. This isn't a violation of fundamental principles, but rather a demonstration of how information itself becomes a resource in probing quantum systems, with implications extending to the very foundations of knowledge acquisition and the limits of predictability in the universe - suggesting that the act of observation, and the information retained, are inextricably linked to the quantum realm.
The observed interplay between entanglement and spacetime curvature extends beyond the immediate concerns of quantum communication, reaching into the foundational challenges of quantum gravity. These results suggest that spacetime may not be a passive backdrop for quantum phenomena, but an active participant, fundamentally altering quantum correlations. This interplay necessitates a re-evaluation of existing theoretical frameworks, potentially requiring modifications to general relativity or the standard model of particle physics to accommodate the observed deviations from established quantum behavior in curved spacetime. Ultimately, a deeper understanding of these effects could provide crucial insights into the long-sought unified theory - a framework capable of seamlessly integrating quantum mechanics and gravity, and resolving persistent paradoxes like the black hole information problem by revealing the true nature of spacetime at the Planck scale.
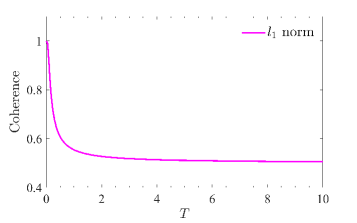
The pursuit of elegant theoretical bounds, like the generalized entropic uncertainty relation detailed in this work, invariably runs headfirst into the messy reality of implementation. It’s almost predictable. The paper meticulously constructs these relationships between uncertainty, coherence, and the spacetime around a Schwarzschild black hole, a beautiful demonstration of interconnectedness. However, one suspects that any attempt to measure these effects will quickly reveal unexpected noise, calibration issues, or unforeseen interactions. As Georg Wilhelm Friedrich Hegel observed, “The truth is the whole.” This holds true here; the ‘whole’ encompassing not just the theoretical framework, but also the limitations of observation and the inherent imperfections of any physical system. The study highlights a connection between uncertainty and entanglement, yet translating this into a reliable, repeatable experiment… that’s a story for another time, and likely another revision of the theory.
What Comes Next?
The derivation of a generalized entropic uncertainty relation, even within the admittedly simplified geometry of a Schwarzschild black hole, feels less like a destination and more like a beautifully crafted set of instructions for building a more complex failure. The relationship established between uncertainty, coherence, and spacetime curvature will undoubtedly prove brittle when confronted with the realities of actual quantum fields in curved spacetime - namely, the infinities that require renormalization, and the approximations that always, eventually, break down. One anticipates the elegant diagrams will require progressively more duct tape.
Future work will inevitably focus on extending this framework to rotating or charged black holes, or perhaps to more exotic geometries. However, it is worth remembering that increasing complexity does not necessarily yield deeper insight. It often merely shifts the location of the inevitable point of failure. The exploration of GHZ states and Hawking radiation as probes of this uncertainty is a promising avenue, yet any practical measurement will be limited by decoherence and the sheer difficulty of isolating quantum systems near event horizons.
Ultimately, the enduring value of this type of research may not lie in its predictive power, but in its ability to refine the questions. Every abstraction dies in production, but at least it dies beautifully. The persistent search for a consistent description of quantum gravity will, at the very least, continue to produce increasingly sophisticated ways to describe the manner in which everything deployable will eventually crash.
Original article: https://arxiv.org/pdf/2602.11503.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Best Controller Settings for ARC Raiders
- Stephen Colbert Jokes This Could Be Next Job After Late Show Canceled
- DCU Nightwing Contender Addresses Casting Rumors & Reveals His Other Dream DC Role [Exclusive]
- 10 X-Men Batman Could Beat (Ranked By How Hard It’d Be)
- 7 Home Alone Moments That Still Make No Sense (And #2 Is a Plot Hole)
- Is XRP ETF the New Stock Market Rockstar? Find Out Why Everyone’s Obsessed!
- Gwen Stefani Details “Blessing” of Her Holidays With Blake Shelton
- 10 Most Brutal Acts Of Revenge In Anime History
- James Gunn & Zack Snyder’s $102 Million Remake Arrives Soon on Netflix
- XRP’s Cosmic Dance: $2.46 and Counting 🌌📉
2026-02-13 12:53