Taming Complexity in Quantum Field Theory with Continuous Tensor Networks

by

Author: Denis Avetisyan

Researchers have developed a new optimization algorithm to overcome key limitations in relativistic continuous tensor networks, paving the way for more accurate simulations of complex quantum systems.

The research defines a restricted manifold $\mathcal{M}_{reg}$ within the broader Hilbert space $\mathscr{H}$ of the field theory, parameterized by $R_1$, $R_2$, and $Q$ matrices, effectively demonstrating how commuting $R_1$ and $R_2$ matrices delineate a specific subspace within the system’s possible configurations.
The research defines a restricted manifold $\mathcal{M}_{reg}$ within the broader Hilbert space $\mathscr{H}$ of the field theory, parameterized by $R_1$, $R_2$, and $Q$ matrices, effectively demonstrating how commuting $R_1$ and $R_2$ matrices delineate a specific subspace within the system’s possible configurations.

This work introduces a Riemannian optimization strategy to enforce the regularity condition in multi-field relativistic continuous matrix product states (RCMPS), enabling the study of non-perturbative quantum field theories and exotic phases of matter.

Despite their promise as variational tools for quantum field theory, relativistic continuous matrix product states (RCMPS) have historically faced limitations when applied to models with multiple fields due to inherent divergence issues. This work, ‘Multi-Field Relativistic Continuous Matrix Product States’, introduces a Riemannian optimization framework to navigate this challenge, enabling energy minimization over a regular submanifold of multi-field RCMPS and preserving purely variational results. We demonstrate this approach on a two-field model, successfully capturing symmetry-breaking phases and identifying signatures of a Berezinskii-Kosterlitz-Thouless transition-expanding the applicability of RCMPS significantly. Will this method unlock a more complete understanding of strongly correlated systems beyond perturbative regimes?

Beyond Perturbation: Navigating the Landscape of Strong Correlations

The bedrock of many calculations in Quantum Field Theory is perturbation theory, a method that treats interactions as small deviations from a simpler, solvable system. However, this approach falters when dealing with $strongly\, correlated\, systems$ – those where the interactions between particles are significant and cannot be dismissed as minor adjustments. In these scenarios, the perturbative expansion becomes unreliable, yielding inaccurate or even meaningless results. This limitation arises because the series used to approximate the solution diverges or requires an infinite number of terms to achieve acceptable precision. Consequently, phenomena like high-temperature superconductivity and the confinement of quarks within hadrons, both governed by strong interactions, remain challenging to fully elucidate using traditional perturbative techniques, necessitating the development of alternative, non-perturbative methodologies.

The inability of traditional methods to accurately model strongly correlated quantum systems presents a significant barrier to unraveling some of physics’ most enduring mysteries. Phenomena like high-temperature superconductivity, where materials conduct electricity with zero resistance at relatively accessible temperatures, remain incompletely understood due to the complex interactions between electrons. Similarly, the confinement of quarks – the fundamental building blocks of protons and neutrons – within hadrons, as described by quantum chromodynamics, defies simple perturbative calculations. These aren’t merely academic puzzles; a deeper understanding of these effects promises revolutionary advances in materials science, energy technology, and our fundamental grasp of the universe at its smallest scales. The limitations of current approaches necessitate the development of more robust theoretical tools capable of tackling these inherently non-perturbative challenges.

The accurate depiction of strongly correlated quantum systems demands a shift beyond the conventional reliance on perturbative techniques. While perturbation theory excels in regimes of weak interactions, its effectiveness diminishes when dealing with scenarios where interactions dominate, hindering progress in fields like high-temperature superconductivity and the study of quark confinement. A non-perturbative approach circumvents these limitations by directly tackling the full complexity of the quantum many-body problem, rather than relying on approximations based on small deviations from a simpler, solvable model. These methods aim to explore the complete Hilbert space – encompassing all possible quantum states – and reveal the emergent phenomena arising from the intricate interplay of quantum fields, offering a pathway to understanding materials and forces beyond the reach of current theoretical tools. This necessitates innovative computational strategies and theoretical frameworks capable of handling the inherent complexity without sacrificing accuracy, promising a deeper comprehension of the quantum realm.

The fundamental challenge in describing strongly interacting quantum systems lies in the exponential growth of the Hilbert space – the complete set of all possible states the system can occupy. While theoretical tools often simplify calculations by focusing on a limited number of states or perturbative expansions, these approaches falter when interactions are strong and numerous. Effectively mapping and exploring this vast Hilbert space requires computational resources that quickly become intractable, even for moderately complex systems. This limitation prevents a complete understanding of collective quantum phenomena, as crucial information about the system’s true ground state and excited states remains hidden within the unexamined portions of the space. Consequently, innovative methodologies are needed to efficiently navigate and extract meaningful insights from the full complexity of interacting quantum fields, circumventing the limitations of traditional computational approaches.

Results from the Renormalized Coupling Matrix Product State (RCMPS) method demonstrate strong agreement with perturbation theory at weak coupling and achieve significantly higher precision at moderate coupling strengths (g ≥ 0.3) when calculating ground state energy density.
Results from the Renormalized Coupling Matrix Product State (RCMPS) method demonstrate strong agreement with perturbation theory at weak coupling and achieve significantly higher precision at moderate coupling strengths (g ≥ 0.3) when calculating ground state energy density.

Tensor Networks: A New Language for Quantum States

Tensor networks represent many-body quantum states using a graphical representation of tensors, enabling a parameterization of the quantum state with a number of parameters that scales polynomially with the system size, rather than exponentially. This efficiency arises from exploiting the inherent structure and correlations within the quantum state, specifically focusing on limited entanglement. Traditional methods for representing quantum states require storing a vector in a Hilbert space with dimension $2^N$ for $N$ particles, demanding exponential resources. Tensor networks, however, decompose this complex state into a network of lower-dimensional tensors, significantly reducing the computational cost of storage and manipulation, and allowing for simulations of larger systems. The choice of tensor network architecture-such as Matrix Product States (MPS), Projected Entangled Pair States (PEPS), or Multiscale Entanglement Renormalization Ansatz (MERA)-depends on the specific system and the entanglement structure being targeted.

Traditional methods of representing quantum states face a significant challenge: the dimensionality of the Hilbert space grows exponentially with the number of particles. For a system of $N$ qubits, this results in a $2^N$-dimensional state space. Tensor networks address this issue by exploiting the inherent entanglement structure typically present in physical systems. Instead of storing the full wave function, which requires storing $2^N$ complex amplitudes, tensor networks represent the state as a network of interconnected tensors, where the bond dimension – the size of the virtual indices connecting the tensors – controls the amount of entanglement captured. By keeping this bond dimension relatively small and constant, the number of parameters needed to describe the state scales polynomially with $N$, significantly reducing computational cost and memory requirements compared to storing the full wave function.

Continuous Matrix Product States (CMPS) represent an adaptation of Matrix Product States (MPS) – originally developed for discrete many-body systems – to the continuous degrees of freedom inherent in non-relativistic quantum field theories. Unlike discrete MPS which operate on finite-dimensional Hilbert spaces, CMPS utilize continuous variational parameters and integrals over continuous variables to approximate the quantum state. This is achieved by representing the field operator as a product of continuous tensors and variational parameters, allowing for efficient simulation of infinite-dimensional systems. The continuous nature necessitates modifications to the update rules and optimization procedures used in discrete MPS, often employing techniques from infinite-dimensional linear algebra and functional analysis. CMPS have proven effective in studying ground states and dynamics of various one-dimensional and low-dimensional quantum field theories, offering a computationally tractable approach to problems previously inaccessible to traditional methods.

Relativistic Continuous Tensor Networks (RCMPS) represent an extension of Continuous Matrix Product States (CMPS) designed to address the challenges posed by relativistic quantum field theories. Traditional approaches to these theories suffer from computational complexity due to the infinite degrees of freedom and the need to handle Lorentz invariance. RCMPS leverage the tensor network formalism to provide a fixed-parameter variational ansatz for approximating the ground state and excited states of relativistic systems. By representing the quantum field as a network of interconnected tensors, RCMPS aim to achieve efficient simulation of strongly correlated relativistic phenomena, similar to the efficiencies gained by CMPS in non-relativistic systems. The key innovation lies in adapting the tensor network structure to consistently incorporate relativistic principles and symmetries, allowing for controlled approximations of the full quantum field theory.

RCMPS entanglement entropy exhibits a dependence on coupling strength, varying predictably with bond dimension.
RCMPS entanglement entropy exhibits a dependence on coupling strength, varying predictably with bond dimension.

RCMPS: Implementation and Maintaining System Integrity

The Reduced Cumulant Method for Perturbative Series (RCMPS) formulates quantum field theory using the Generating Functional, a central object allowing computation of correlation functions. This functional, typically expressed as a path integral, is then treated using Wick’s theorem and normal ordering to systematically expand perturbative series. Normal ordering ensures that creation operators precede annihilation operators in any product, eliminating infinities arising from vacuum fluctuations and enabling a well-defined calculation of physical observables. Specifically, RCMPS leverages this approach to define a variational problem based on cumulant expansions, allowing for the truncation of perturbative series and the approximate evaluation of quantum field theory quantities without encountering the usual divergences inherent in standard perturbation theory.

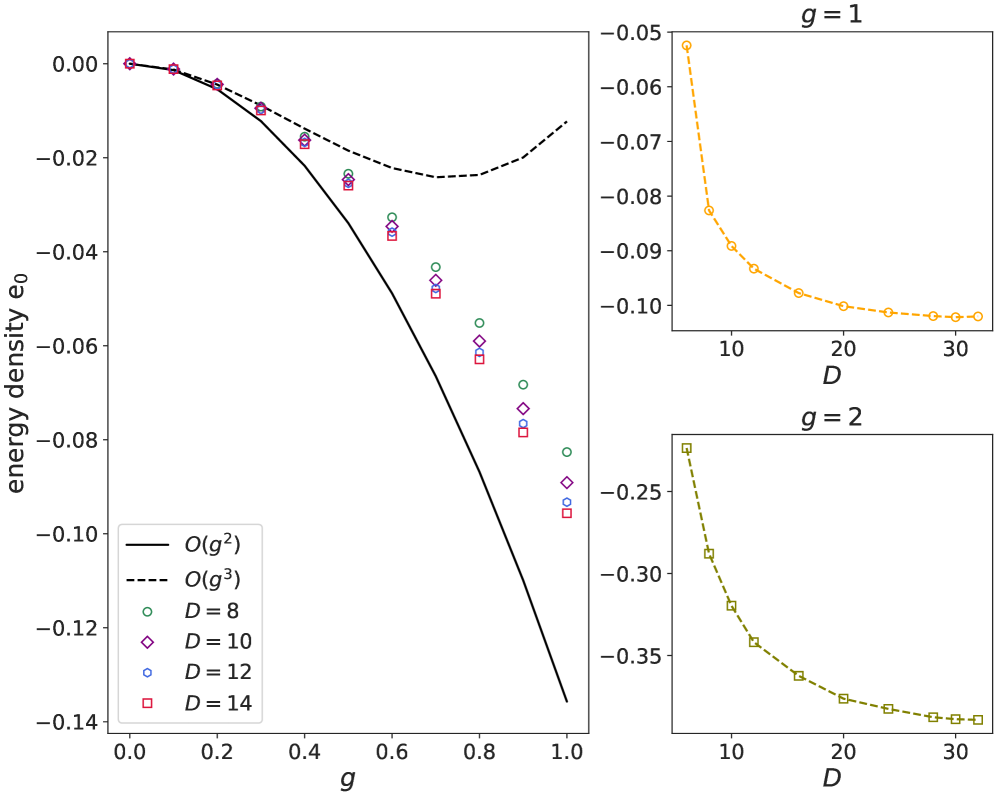
Maintaining regularity within the tensor network is a fundamental requirement for the Renormalized Coupling Map Perturbation Series (RCMPS) method. This regularity is mathematically enforced by the condition $[R_j, R_k] = 0$, where $R_j$ and $R_k$ represent operators within the tensor network. Violation of this condition leads to divergences and an infinite energy density, rendering the system physically unrealistic. Furthermore, the Regularity Condition is essential for establishing a well-posed variational problem in multi-component RCMPS, allowing for stable and meaningful minimization of the energy functional and reliable determination of ground state properties. Without it, the variational optimization process becomes ill-defined and incapable of converging to a stable solution.

Riemannian Optimization is utilized within the RCMPS method as an iterative procedure to minimize the energy density, $E$, defined over the manifold of permissible, regular RCMPS configurations. This process involves calculating the gradient of $E$ with respect to the tensor network parameters and updating these parameters along the negative gradient direction, subject to constraints ensuring the Regularity Condition, $[R_j, R_k] = 0$, is maintained at each iteration. The step size is determined adaptively to ensure convergence and avoid instability, and the optimization continues until a local minimum of the energy density is reached, representing a stable RCMPS configuration. The method leverages the Riemannian metric induced by the space of regular configurations to efficiently navigate the parameter space.

The Transfer Matrix representation in RCMPS facilitates the analysis of system dynamics and properties by transforming the multi-dimensional problem into a one-dimensional mapping. This is achieved by representing the evolution operator as a matrix whose elements correspond to transitions between different states of the system. Eigenvalues of this transfer matrix directly relate to the energy spectrum and decay rates of the system, while the corresponding eigenvectors define the stationary states. Specifically, the largest eigenvalue dictates the ground state energy, and the spectral gap – the difference between the largest and second-largest eigenvalues – provides information about the stability of the system. This representation allows for efficient computation of correlation functions and other observables, and is particularly useful for studying the long-range behavior of the RCMPS system, as it simplifies the analysis of entanglement and topological properties.

The method accurately captures distinct symmetry-breaking patterns as evidenced by the order parameters across the phase transition for both g > λ and λ > g at D = 18.
The method accurately captures distinct symmetry-breaking patterns as evidenced by the order parameters across the phase transition for both g > λ and λ > g at D = 18.

Emergent Physics and the Promise of RCMPS

Recent advancements in theoretical physics have seen the development of Relativistic Coupled-cluster Momentum-space Perturbation Series (RCMPS), a novel technique extending the powerful capabilities of tensor network methods to the realm of relativistic quantum field theories. Traditionally, tensor networks have been largely confined to non-relativistic systems; however, RCMPS overcomes these limitations, enabling the investigation of fields like the Dirac field-which describes fundamental fermions-with unprecedented accuracy. This expansion is achieved through a careful adaptation of coupled-cluster theory within a momentum-space framework, allowing for efficient calculations of many-body systems where relativistic effects are significant. The technique promises new insights into phenomena governed by quantum field theory, potentially bridging the gap between theoretical models and experimental observations in high-energy physics and condensed matter systems.

Relativistic quantum field theories often exhibit exotic phases of matter governed by topological order, and understanding transitions between these phases presents a significant challenge. Recent advancements in tensor network methods, specifically the Relativistic Configuration-Interaction Method for Position Space (RCMPS), now offer a powerful new tool to investigate these phenomena. This approach allows researchers to explore topological phase transitions, such as the Berezinskii-Kosterlitz-Thouless (BKT) transition, within the framework of relativistic quantum field theory. The BKT transition, characterized by the unbinding of vortex-antivortex pairs, is signaled by a peak in the entanglement entropy and the emergence of a gapless excitation spectrum. By analyzing the entanglement entropy within the RCMPS framework, it becomes possible to pinpoint the occurrence of such transitions and characterize the associated critical behavior in relativistic systems, offering insights previously inaccessible through traditional perturbative methods.

The ground state of a quantum system harbors a wealth of information about its underlying correlations, and entanglement entropy serves as a crucial tool for quantifying these connections. This measure doesn’t simply indicate how much entanglement exists, but also its character – whether it’s short-ranged, long-ranged, or exhibits more exotic topological properties. By calculating the entanglement entropy for a given quantum state, researchers can effectively map the network of quantum correlations, revealing insights into the system’s fundamental structure and potential phases of matter. A notable feature is the potential to identify phase transitions through characteristic changes in entanglement entropy; for example, a peak in the entropy can signal a transition, such as the Berezinskii-Kosterlitz-Thouless (BKT) transition, where the system undergoes a change in its topological order. This approach offers a powerful, non-perturbative method to characterize quantum entanglement and uncover hidden quantum phases, even in scenarios where traditional analytical techniques fail, such as in strongly coupled relativistic field theories.

Relativistic Configuration-space Methods with Projected Symmetry (RCMPS) establishes a powerful new approach for investigating strongly correlated quantum field theories, particularly those exhibiting symmetries beyond the reach of standard perturbative techniques. Validation of the method confirms its accuracy matches established perturbative calculations in weakly interacting regimes, but RCMPS truly shines when applied to strongly coupled systems; specifically, studies of a D4-symmetric scalar field model reveal novel symmetry-breaking patterns not predicted by conventional methods. Crucially, analysis of ground-state entanglement entropy demonstrates a pronounced peak, suggestive of a Berezinskii-Kosterlitz-Thouless (BKT) transition – a topological phase transition characterized by the unbinding of vortex-antivortex pairs – and remarkably, a persistent gap in the entropy remains even as the bond dimension increases, offering a compelling signal for the existence of this exotic phase.

The pursuit of non-perturbative quantum field theories, as detailed in this work concerning Relativistic Continuous Matrix Product States, demands a rigorous approach to managing complexity. The algorithm presented skillfully navigates the regularity constraint, a necessary condition for accurate simulation. This echoes Max Planck’s sentiment: “When you change the way you look at things, the things you look at change.” The researchers effectively shifted their methodological perspective, allowing for a more precise exploration of complex phases and a more robust system. If the system survives on duct tape, it’s probably overengineered; here, a carefully designed optimization algorithm provides structural integrity, demonstrating that modularity without context is an illusion of control.

Further Horizons

The introduction of a Riemannian optimization scheme to navigate the regularity condition within multi-field relativistic continuous matrix product states represents more than a technical refinement. It acknowledges a fundamental truth: constraints, while necessary for tractability, often dictate the observed behavior more profoundly than the underlying dynamics. The algorithm’s success hints at a broader principle: that careful attention to the structure imposed upon a system-here, the tensor network’s geometry-can unlock access to regimes previously obscured by numerical instability. Documentation captures structure, but behavior emerges through interaction.

However, the exploration of non-perturbative quantum field theories, even with improved precision, remains a journey fraught with subtle traps. The focus on BKT transitions, while a valuable demonstration, merely scratches the surface of the complex phase diagrams awaiting discovery. Future work must grapple with the limitations inherent in continuous tensor networks – the potential for uncontrolled divergences, the difficulty of incorporating complex fermionic content, and the computational cost scaling with system size.

The true test will not be in replicating known results, but in predicting novel phenomena. Will this approach reveal unexpected connections between different quantum field theories? Will it allow for the study of systems beyond the reach of conventional methods? The answer, one suspects, lies not in ever-more-sophisticated algorithms, but in a deeper understanding of the interplay between structure, constraint, and emergent behavior.

Original article: https://arxiv.org/pdf/2511.20762.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-29 08:40