Taming Quantum Chaos: A Stochastic Approach to Many-Body Dynamics

by

Author: Denis Avetisyan

New research critically examines the limits of simulating complex quantum systems using stochastic trajectories, revealing challenges in long-term stability.

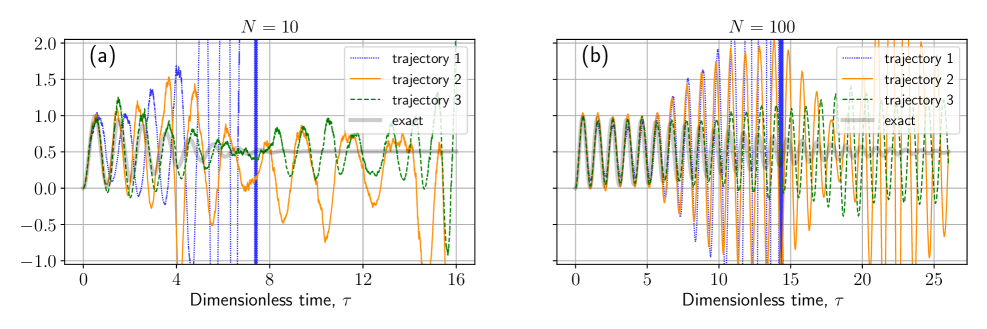
The simulation tracks the stochastic variable $\rho_{ee}$ alongside the exact solution for excited state probability within a closed two-color maser, demonstrating that even with zero dissipation ($\gamma/f = 0$) and starting from the ground state, the system’s evolution—observed across both ten and one hundred atoms—reveals inherent probabilistic fluctuations alongside a deterministic trajectory.
The simulation tracks the stochastic variable $\rho_{ee}$ alongside the exact solution for excited state probability within a closed two-color maser, demonstrating that even with zero dissipation ($\gamma/f = 0$) and starting from the ground state, the system’s evolution—observed across both ten and one hundred atoms—reveals inherent probabilistic fluctuations alongside a deterministic trajectory.

This review assesses the performance of stochastic trajectory methods applied to the Tavis-Cummings model, exploring techniques to address trajectory divergence and improve simulation accuracy.

Simulating many-body quantum dynamics remains a significant challenge, particularly for systems exhibiting strong quantum features. This is critically examined in ‘Modelling many-body quantum dynamics with stochastic trajectories: a critical test on the Tavis-Cummings model’, where the authors investigate the applicability of a stochastic trajectory method to the Tavis-Cummings model. Their analysis reveals that divergent trajectories limit the timeframe for accurate simulations, despite attempts to regularize these instabilities through techniques like dissipation and drift-gauge transformations. Ultimately, the study questions the general feasibility of stochastic phase-space sampling for capturing the full quantum evolution of strongly correlated systems—can alternative approaches overcome these fundamental limitations and unlock efficient, long-time simulations of complex quantum phenomena?

help

The Illusion of Control: Modeling Open Quantum Systems

Describing open quantum systems—those interacting with their environment—is inherently complex, demanding approximations to manage intractable dimensionality. This stems from the infinite degrees of freedom in representing both the system and its surroundings, necessitating reduced models and careful consideration of environmental effects. Traditional approaches, like solving the Quantum Master Equation, quickly become computationally prohibitive. Alternative techniques exist, but each carries its own limitations. Accurately capturing environmental noise is a key difficulty, as its precise form significantly affects dynamics. Incorrect modeling leads to inaccurate predictions and a misunderstanding of the underlying physics.

Analysis of trajectory behavior reveals that, with $N=100$ particles and varying photon numbers, the closed three-mode cascaded (TCM) system maintains all trajectories until a threshold of 0.5% runaway trajectories is reached, while the open TCM system exhibits differing behavior based on the value of $\gamma$, with lower $\gamma$ values leading to converged results.
Analysis of trajectory behavior reveals that, with $N=100$ particles and varying photon numbers, the closed three-mode cascaded (TCM) system maintains all trajectories until a threshold of 0.5

Ultimately, the pursuit of understanding these systems feels like tracing photons lost beyond the event horizon—a humbling reminder that even our most elegant models are, by necessity, incomplete.

Simulating the Quantum Realm: Stochastic Trajectories

The StochasticTrajectoryMethod offers a computational technique for simulating quantum dynamics, utilizing models based on StochasticDifferentialEquations. This approach bypasses direct Schrödinger equation solving by mapping quantum evolution onto an ensemble of classical trajectories, each incorporating noise to represent quantum fluctuations. Its reliance on ItoCalculus ensures mathematical rigor, while leveraging classical computation offers efficiency.

With $N=10$ particles and varying photon numbers, the closed three-mode cascaded (TCM) system preserves all trajectories until 0.5% become unstable, while the open TCM system's behavior is modulated by the parameter $\gamma$, where lower values promote convergence.
With $N=10$ particles and varying photon numbers, the closed three-mode cascaded (TCM) system preserves all trajectories until 0.5

This technique allows for simulations of complex quantum systems otherwise intractable. By calibrating the noise term and utilizing ItoCalculus, researchers approximate quantum dynamics, opening new avenues for exploring matter at the quantum level.

Taming Chaos: Drift, Dissipation, and Stability

Uncontrolled stochastic simulations are prone to RunawayTrajectories, introducing inaccuracies and instability. These arise from inherent randomness and can quickly diverge from plausible solutions. The DriftGaugeTransformation controls these behaviors by modifying the deterministic component of the StochasticDifferentialEquation, stabilizing the simulation without altering expectation values. Furthermore, incorporating Dissipation, via the QuantumMasterEquation, acts as a regularizing mechanism, promoting both stability and physical relevance.

Comparison of weighted and non-weighted averages of the stochastic variable $\rho_{ee}$ with its actual value and the switch function demonstrates their relationship as a function of dimensionless time, with distinct behaviors observed for $\gamma/f=0$ and $\gamma=2.6f$ and parameters $x_1=-1$, $x_2=2$, and $k=1.
Comparison of weighted and non-weighted averages of the stochastic variable $\rho_{ee}$ with its actual value and the switch function demonstrates their relationship as a function of dimensionless time, with distinct behaviors observed for $\gamma/f=0$ and $\gamma=2.6f$ and parameters $x_1=-1$, $x_2=2$, and $k=1.

Analysis indicates a damping parameter of $\gamma/f = 2.6$ is required for stable simulations. This dissipation absorbs energy, preventing runaway trajectories and grounding the simulation in realistic dynamics.

The Limits of Approximation: Where Models Begin to Fail

The StochasticTrajectoryMethod, combined with dimensionality reduction techniques like PermutationalSymmetry, facilitates efficient simulations of complex quantum systems. This is particularly valuable for investigating models like the TavisCummingsModel, describing the interaction between a single electromagnetic field mode and a collection of two-level atoms. Investigations reveal insights into the SemiClassicalLimit, where quantum effects diminish. Accurate characterization of statistical relationships via the CorrelationFunction is essential for model validation, as is understanding the properties of the NoiseTerm arising from stochastic simulations.

The effective potential and Hamiltonian, as defined in equation (16), exhibit a specific functional relationship as a function of population inversion $w$.
The effective potential and Hamiltonian, as defined in equation (16), exhibit a specific functional relationship as a function of population inversion $w$.

Analysis of excited state probability reveals a second-order dependence in the divergence of its second derivative, suggesting a subtle interplay between quantum fluctuations and classical dynamics as the system approaches a critical point. Like any map pushed to its limits, the model’s clarity fades as it nears the horizon of its own assumptions.

The presented work delves into the complexities of modelling many-body quantum dynamics, revealing inherent limitations within the stochastic trajectory method as simulations extend in time. The emergence of divergent trajectories underscores the delicate balance between approximation and accuracy, a challenge reminiscent of confronting the event horizon of a black hole – beyond which established methods lose their predictive power. As John Bell keenly observed, “No physical theory should be rejected until it has been pushed to the limits of its applicability.” This research rigorously tests those limits, exploring dissipation and drift-gauge transformations as potential means of mitigating divergence and extending the reach of the method, much like attempting to peer beyond that horizon with increasingly refined instruments.

What Lies Beyond the Trajectory?

The exercise of modelling quantum dynamics with stochastic trajectories, as demonstrated by this work with the Tavis-Cummings model, isn’t a quest for precision. It is, rather, a careful charting of the limits of representation. The divergence of trajectories, the need for artifice like dissipation and gauge transformations to hold simulations together—these aren’t merely technical hurdles. They are signposts indicating where the map dissolves. Every corrective measure, every attempt to tame the chaos, implicitly acknowledges the incompleteness of the initial assumptions.

Future work will undoubtedly refine the techniques for managing these divergent paths. More sophisticated dissipation schemes, adaptive sampling methods—these will push the boundaries of simulation time, certainly. But the fundamental question remains: what is being lost in the taming? Is the price of a longer trajectory the suppression of genuinely novel, unrepresentable behaviours? Discovery isn’t a moment of glory; it’s realizing how little is known.

Perhaps the true path forward lies not in building more elaborate simulations, but in accepting the inherent limitations of any such endeavour. Everything called law can dissolve at the event horizon. The challenge isn’t to predict the unpredictable, but to understand the nature of that unpredictability itself, to map the boundary between knowledge and the unknowable, even if that boundary is forever receding.

Original article: https://arxiv.org/pdf/2511.08815.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

See also:

2025-11-13 15:18