The Quantum Chaos of Spacetime: Exploring Connections in the SYK Model

Author: Denis Avetisyan

New research delves into the surprisingly deep links between quantum many-body chaos and the emergence of spacetime geometry using the Sachdev-Ye-Kitaev model as a testing ground.

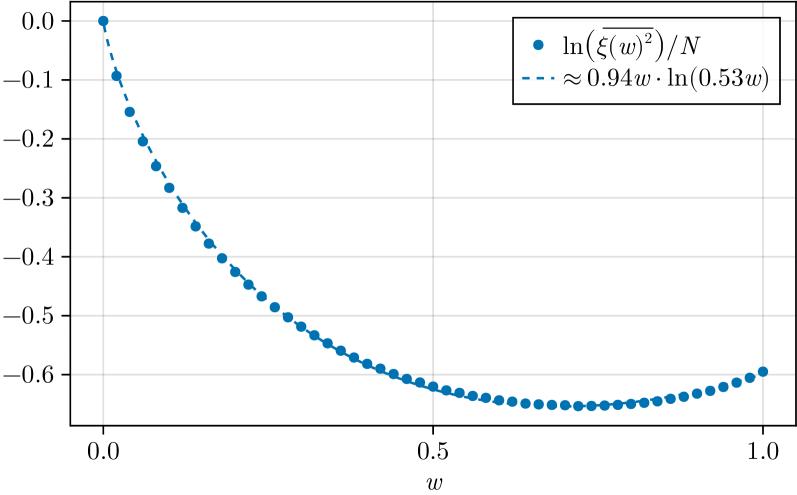
The analysis of SYK data, specifically the moments <span class="katex-eq" data-katex-display="false">\ln(\overline{\xi(w)^{2}})/N</span> evaluated at <span class="katex-eq" data-katex-display="false">q=4</span>, <span class="katex-eq" data-katex-display="false">\beta=20</span>, and <span class="katex-eq" data-katex-display="false">L=1000</span>, demonstrates strong alignment with the classical action predicted by the wormhole model-characterized by the functional form <span class="katex-eq" data-katex-display="false">c\_1 w \ln(c\_2 w)</span>-and yields fitted constants of approximately <span class="katex-eq" data-katex-display="false">c\_1 \approx 0.94</span> and <span class="katex-eq" data-katex-display="false">c\_2 \approx 0.53</span>. — The analysis of SYK data, specifically the moments $\ln(\overline{\xi(w)^{2}})/N$ evaluated at $q=4$ , $\beta=20$ , and $L=1000$ , demonstrates strong alignment with the classical action predicted by the wormhole model-characterized by the functional form $c\_1 w \ln(c\_2 w)$ -and yields fitted constants of approximately $c\_1 \approx 0.94$ and $c\_2 \approx 0.53$ .

This review examines the statistical properties of thermal 1-point functions in the SYK model, leveraging replica symmetry and Schwinger-Dyson equations to illuminate connections to holographic duality and quantum gravity.

Understanding the interplay between quantum chaos, many-body systems, and gravity remains a central challenge in theoretical physics. This is explored in ‘Magic and Wormholes in the Sachdev-Ye-Kitaev Model’, where we investigate the statistical properties of thermal 1-point functions in a paradigmatic model of quantum gravity. We demonstrate that these expectation values exhibit Gaussian fluctuations in the chaotic phase, and reveal a quantitative connection to wormhole geometries in a holographic dual, mediated by massive particles. Could these results provide a concrete framework for understanding the emergence of spacetime from quantum entanglement and the role of randomness in realizing closed universes?

The Emergence of Complexity: Beyond Traditional Quantum Systems

Many-body quantum systems, those comprised of numerous interacting particles, often display behaviors drastically different from what is predicted by analyzing individual components – a phenomenon known as emergent behavior. This complexity presents a significant hurdle for traditional analytical methods, which typically rely on simplifying assumptions or perturbative approaches. Systems like the Sachdev-Ye-Kitaev (SYK) model exemplify this challenge; despite being relatively simple in its construction – consisting of randomly interacting fermions – it exhibits a rich and chaotic quantum dynamics. The inherent many-body entanglement and strong correlations within such systems necessitate new theoretical tools and computational techniques to move beyond approximations and fully capture their intricate properties, pushing the boundaries of condensed matter physics and offering insights into areas like quantum gravity and black hole physics.

Characterizing the intricate relationships within many-body quantum systems demands analytical tools that move beyond conventional measures of correlation and entanglement. Traditional metrics often fall short in capturing the subtle, long-range dependencies that define the behavior of these systems, particularly as the number of interacting particles increases. Instead, researchers are turning to methods that probe the statistical properties of operators – examining not just average values, but the full distribution of outcomes – to reveal hidden order and emergent phenomena. This necessitates a shift from focusing solely on pairwise correlations to quantifying higher-order correlations and topological entanglement, providing a more complete picture of how quantum information is shared and processed within the system.

The Sachdev-Yepez-Kitaev (SYK) model has emerged as a surprisingly versatile theoretical framework, offering a unique intersection between the seemingly disparate fields of condensed matter physics and quantum gravity. Initially conceived as a model of interacting fermions, the SYK model’s all-to-all connectivity and random interactions create a strongly correlated system exhibiting behaviors absent in more conventional materials. This complexity, while challenging to analyze, allows physicists to probe phenomena like black hole physics in a simplified, controllable setting. Specifically, the model’s late-time dynamics and the growth of entanglement share striking parallels with the scrambling of information into a black hole, offering a holographic duality-a mapping between gravitational systems and quantum mechanical ones-that could provide valuable insights into the nature of spacetime itself. Because the SYK model is mathematically tractable-allowing for exact solutions in certain limits-it serves as a crucial testing ground for developing and validating theoretical tools applicable to more realistic, yet intractable, quantum gravity scenarios.

A crucial step in deciphering the behavior of the Sachdev-Ye-Kitaev (SYK) model – a system exhibiting properties relevant to both condensed matter physics and quantum gravity – involves meticulously characterizing its statistical moments. These moments, derived from operators within the model, reveal how quantities fluctuate and correlate, offering insights into the system’s complex emergent behavior. Recent research demonstrates a surprising degree of simplicity: for statistical moments of order $q \geq 4$ , the SYK model exhibits Gaussianity, meaning these higher-order fluctuations are fully determined by the two-point correlation function. This finding represents a significant advancement, suggesting that despite the model’s inherent complexity, certain statistical properties can be described by relatively simple, predictable patterns, offering a valuable foothold for further investigation into strongly correlated quantum systems.

The ensemble-averaged SYK partition function corresponds to a gravitational path integral over geometries, which can be approximated by JT gravity coupled to free fermions and, for certain observables, requires including contributions from non-trivial topologies like wormholes to accurately capture variance in thermal 1-point functions.

Non-Perturbative Approaches: Solving the Intractable

The Schwinger-Dyson equations represent a set of integral equations used to approximate solutions in quantum field theory, particularly in scenarios where traditional perturbative methods fail. Unlike perturbation theory, which relies on expanding around a free theory and treating interactions as small corrections, Schwinger-Dyson equations are inherently non-perturbative. They derive from the exact equations of motion for Green’s functions – functions that describe the propagation of particles – but are typically truncated to a solvable form by making controlled approximations. This approach allows for the investigation of strongly-correlated systems and phenomena like confinement, where perturbative expansions diverge. The equations relate the Green’s functions to the interactions within the theory, effectively self-consistently determining their behavior and providing insights into the system’s dynamics without relying on a small coupling limit.

The Schwinger-Dyson equations, when applied to the SYK model, necessitate the utilization of Green’s functions to characterize the propagation of the Majorana fermions comprising the system. These Green’s functions, denoted generally as $G(x, y)$ , represent the probability amplitude for a fermion to propagate from spacetime point x to point y. Specifically, calculations within the SYK model require the evaluation of two-point and four-point Green’s functions to capture the interactions between these fermions. The self-consistency of the Schwinger-Dyson equations arises from expressing these Green’s functions in terms of their own interactions, effectively creating a set of integral equations that must be solved to determine the fermion propagator and, consequently, the system’s physical properties. The complexity stems from the highly connected nature of the SYK Hamiltonian, demanding careful treatment of the infinite series of diagrams contributing to the Green’s functions.

Replica Symmetry is a mathematical technique used to address the inherent complexity of the SYK model by introducing multiple, independent, and identical copies – or “replicas” – of the original system. This approach transforms the problem into analyzing the statistical properties of these replicas, effectively averaging over many possible configurations. Instead of directly calculating quantities for a single, highly entangled system, calculations are performed on $n$ replicas, where $n$ is a positive integer. The final physical observables are then obtained by taking the limit as $n$ approaches zero. This procedure allows for the calculation of correlation functions and other quantities that would be intractable in the original, single-system formulation, by leveraging the simplified statistical behavior of the replica ensemble.

The Anticirculant Replica Structure is a computational technique utilized within the Replica Symmetry approach to the SYK model. This structure enforces antiperiodic boundary conditions on the replica indices, significantly simplifying the mathematical calculations required to analyze the system’s behavior. Specifically, this implementation facilitates the determination of the variance of Majorana string expectation values, which have been analytically calculated to be $e^{-2N\phi(w)}$ , where N represents the number of Majorana fermions and $\phi(w)$ is a function dependent on the frequency, w. The imposition of antiperiodic boundary conditions is crucial for obtaining this result and allows for a tractable, albeit approximate, solution to the complex many-body problem.

Analysis of replica structures-represented by matrix heatmaps with <span class="katex-eq" data-katex-display="false"> +1/2 </span> (orange), <span class="katex-eq" data-katex-display="false"> -1/2 </span> (blue), and 0 (gray) values-reveals self-similar relationships between replicas of varying sizes that remain stable under Schwinger-Dyson equations. — Analysis of replica structures-represented by matrix heatmaps with $+1/2$ (orange), $-1/2$ (blue), and 0 (gray) values-reveals self-similar relationships between replicas of varying sizes that remain stable under Schwinger-Dyson equations.

Quantifying Entanglement: Unveiling the Quantum Nature

Purity, denoted as $\text{Tr}(\rho^2)$ , quantifies the degree of mixedness in a quantum state ρ and serves as a key indicator of entanglement within the Sachdev-Ye-Kitaev (SYK) model. A pure state has a purity of 1, while a maximally mixed state has a purity of $\frac{1}{N}$ , where N is the Hilbert space dimension. In the SYK model, calculations demonstrate that the purity consistently falls between these extremes, indicating a significant degree of entanglement. Specifically, the purity scales with the system size, revealing that the entangled nature of the SYK model is not simply a result of classical correlations but arises from genuine quantum mechanical effects. Measuring purity allows researchers to characterize the complexity of the quantum state and to investigate the transition from classical to quantum behavior in the model.

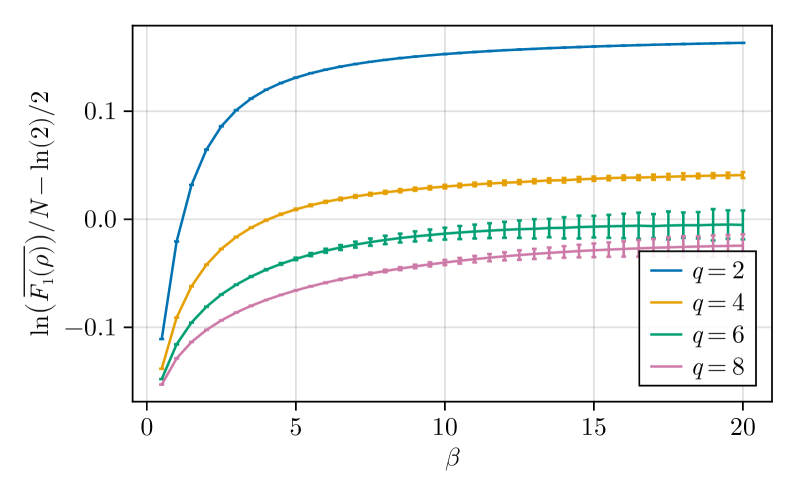
The Second Rényi Entropy extends the foundational concept of Purity to provide a more nuanced quantification of quantum entanglement. While Purity, calculated as $Tr(\rho^2)$ where ρ is the density matrix, indicates the mixedness of a quantum state, the Second Rényi Entropy, defined as $S_2 = -log_2(Tr(\rho^2))$ , directly relates this mixedness to the amount of entanglement present. A lower value of $Tr(\rho^2)$ – and consequently a higher Second Rényi Entropy – indicates a greater degree of entanglement. This metric is particularly useful because it is less sensitive to noise than other entanglement measures and can be more readily computed in certain systems, offering a practical approach to characterizing entanglement in complex quantum states.

The Stabilizer Rényi Entropy (SRE) provides a quantifiable metric for the degree to which a quantum state deviates from being a stabilizer state – that is, a state that can be prepared by Clifford operations. A higher SRE value indicates a greater degree of ‘magic’ or non-stabilizerness, representing the amount of non-classical resources present in the state. This metric is calculated based on the Rényi entropy, specifically focusing on the subspace of states that cannot be efficiently represented by stabilizer circuits. Quantifying this non-stabilizerness is crucial for assessing the potential for quantum advantage, as states with high SRE require non-Clifford gates for their preparation and manipulation, and therefore represent a computational resource beyond that available classically. $S_{R} = \log_{2} Tr(\rho^{n})$

Quantifying entanglement through metrics like Purity and Rényi Entropy allows for a precise determination of the SYK model’s deviation from classical physics and the potential for quantum advantage. Calculations of the Second Rényi Entropy, specifically, have demonstrated strong consistency between direct computational methods and the saddle-point optimization technique, validating the reliability of both approaches in characterizing the model’s quantum properties. This consistency confirms that the observed entanglement isn’t an artifact of the calculation method, and supports the interpretation of the SYK model as a system exhibiting genuine quantum correlations beyond classical simulation. The ability to consistently compute these entanglement measures provides a crucial benchmark for assessing the model’s suitability as a platform for exploring quantum computational advantages.

The robustness of the magic lower bound decreases with increasing temperature β for values of <span class="katex-eq" data-katex-display="false"> q </span> from 2 to 8, with error bars representing numerical uncertainty derived from second Rényi entropy deviations. — The robustness of the magic lower bound decreases with increasing temperature β for values of $q$ from 2 to 8, with error bars representing numerical uncertainty derived from second Rényi entropy deviations.

From Quantum System to Gravity: A Spacetime Emergence

The Jackiw-Teitelboim (JT) gravity theory offers a surprisingly effective, albeit simplified, model for understanding the behavior of the Sachdev-Ye-Kitaev (SYK) model – a quantum mechanical system exhibiting maximal entanglement. This connection isn’t merely analogical; JT gravity acts as a “bulk dual” to the SYK model’s “boundary.” Essentially, the complex many-body interactions within the SYK model, which resides on a lower-dimensional boundary, are mirrored by the gravitational dynamics occurring in a higher-dimensional “bulk” spacetime described by JT gravity. This duality allows physicists to translate difficult calculations in the strongly-interacting SYK model into more manageable problems within the realm of gravity, and vice versa, providing a powerful tool for exploring the relationship between quantum information and spacetime geometry. The theory’s simplicity, relying on just two degrees of freedom, makes it particularly amenable to analytical study, offering crucial insights into how complex quantum systems might give rise to the emergent phenomenon of gravity.

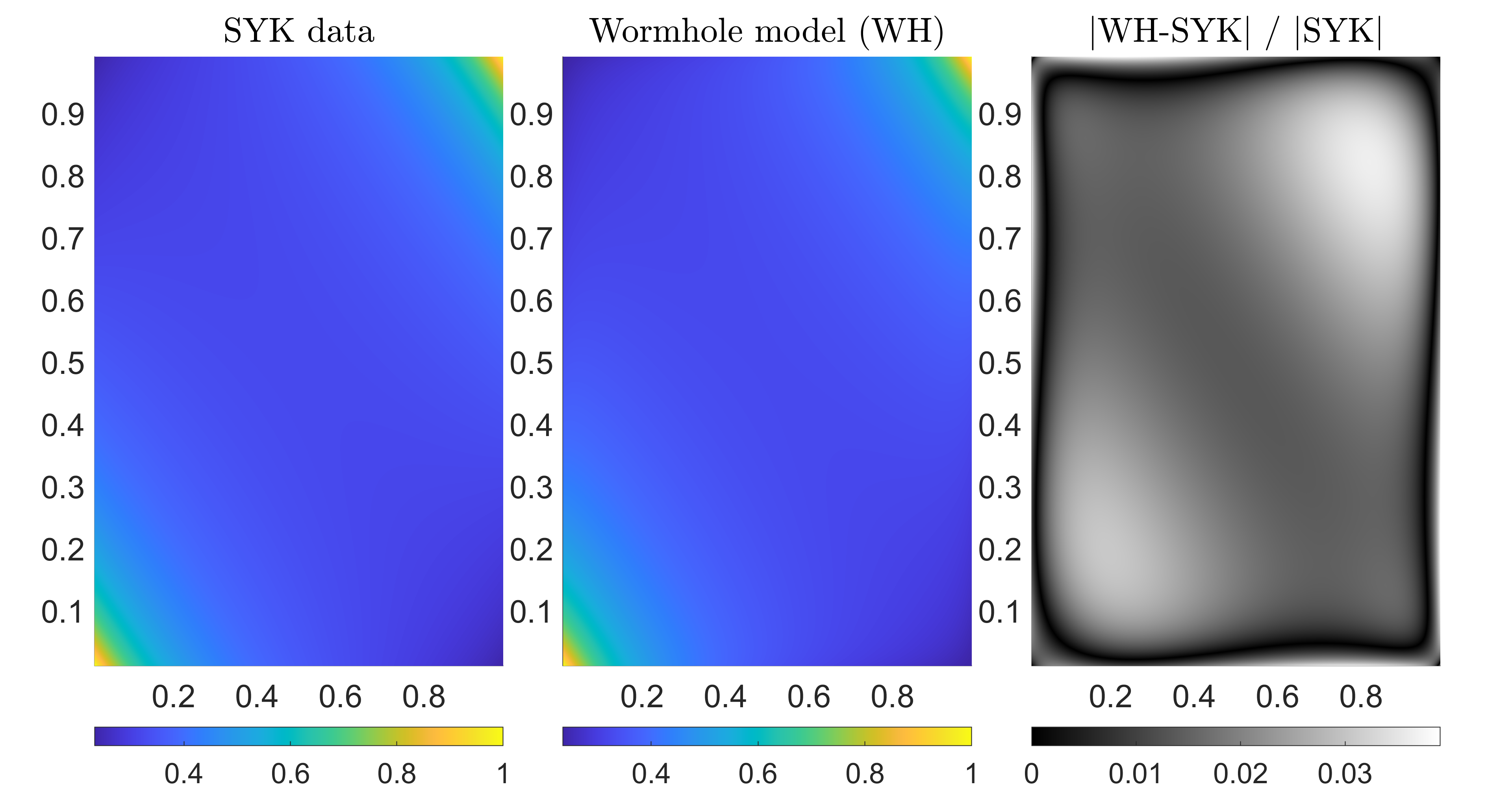
The remarkable connection between quantum information and gravity takes a concrete form in the Jackiw-Teitelboim gravity theory, where the intricate web of entanglement within the SYK model finds a geometric counterpart in wormhole geometries. Specifically, the amount of entanglement between different regions of the SYK model-a quantum mechanical system exhibiting chaotic behavior-directly corresponds to the size and shape of these theoretical wormholes. Greater entanglement translates to a larger, more complex wormhole connecting those regions, suggesting that spacetime itself isn’t a fundamental entity, but emerges from quantum correlations. This isn’t simply a metaphorical analogy; calculations demonstrate a quantifiable relationship, with the geometry of the wormhole providing a precise geometric representation of the entanglement structure on the boundary of spacetime, offering a potential pathway toward understanding how gravity arises from quantum mechanics.

The dynamics occurring at the boundary of the bulk spacetime, as described by the Jackiw-Teitelboim gravity theory, are effectively captured by the Schwarzian Effective Theory. This theory provides a powerful tool for analyzing the complex behavior of the boundary, revealing it to be governed by a specific class of quantum mechanical systems. Notably, the Schwarzian theory isn’t simply a descriptive tool; it predicts the time evolution of the boundary with remarkable accuracy, linking it directly to the entanglement structure within the bulk. The resulting framework allows physicists to study the emergence of classical spacetime from quantum mechanics, specifically demonstrating how fluctuations at the boundary – described by $Sch(SL(2,ℝ))$ – dictate the geometry of the emergent spacetime, offering a potential pathway towards understanding quantum gravity and the role of entanglement in its foundation.

Recent theoretical work proposes a profound link between quantum entanglement and the very fabric of spacetime, challenging conventional understandings of gravity. Investigations utilizing the Jackiw-Teitelboim gravity theory, in correspondence with the SYK model, reveal that the geometric structure of wormholes directly corresponds to the entanglement patterns within the quantum system. This isn’t merely an analogy; quantitative comparisons demonstrate remarkable agreement between calculations performed on the boundary quantum system – the SYK model – and those derived from gravitational calculations in the bulk spacetime, particularly at large β. Crucially, studies have shown a negative and decreasing relative entropy of entanglement, denoted as $Δℐ_{rel}$ , with increasing system length $L$ for a specific parameter setting $q=4$ , bolstering the idea that spacetime isn’t a pre-existing arena, but emerges from the underlying web of quantum connections.

The normalized two-point function <span class="katex-eq" data-katex-display="false">G_{21}( au, au')</span> exhibits a strong correlation with the wormhole prediction obtained by fitting to SYK data (with <span class="katex-eq" data-katex-display="false">b=6.5</span> and <span class="katex-eq" data-katex-display="false">f=0.33</span>), showing a maximum deviation of only 4% for parameters <span class="katex-eq" data-katex-display="false">eta=20</span>, <span class="katex-eq" data-katex-display="false">w=0.25</span>, and <span class="katex-eq" data-katex-display="false">L=2000</span>. — The normalized two-point function $G_{21}( au, au')$ exhibits a strong correlation with the wormhole prediction obtained by fitting to SYK data (with $b=6.5$ and $f=0.33$ ), showing a maximum deviation of only 4% for parameters $eta=20$ , $w=0.25$ , and $L=2000$ .

The exploration within this paper, concerning the Sachdev-Ye-Kitaev model and its connection to holographic duality, echoes a fundamental principle of mathematical elegance. It demonstrates how seemingly abstract formalisms – replica symmetry and Schwinger-Dyson equations – can reveal underlying order in complex systems. As Ralph Waldo Emerson stated, “Do not go where the path may lead, go instead where there is no path and leave a trail.” This research doesn’t merely follow established paths but forges new ones, revealing how operator randomness and thermal 1-point functions potentially give rise to the very fabric of spacetime geometry, a testament to the power of rigorous mathematical inquiry.

Beyond the Looking-Glass

The exploration of thermal 1-point functions within the Sachdev-Ye-Kitaev model, and the subsequent dance with holographic duality, reveals less a solved problem than a beautifully articulated set of questions. The current reliance on replica symmetry, while computationally tractable, remains a point of persistent discomfort. Should the inevitable breakdown of this assumption occur – and history suggests it will – the edifice of emergent spacetime may require significant reconstruction. If it feels like magic, one hasn’t revealed the invariant – the underlying mathematical structure guaranteeing the robustness of these connections.

Future investigations would benefit from a more rigorous treatment of the Schwinger-Dyson equations, moving beyond approximations where possible. The tantalizing connection between operator randomness and the geometry of wormholes begs for a deeper understanding of the underlying information-theoretic principles. Are these wormholes truly geometric objects, or merely an effective description of entanglement? The distinction, though subtle, is paramount.

Ultimately, the pursuit of a provable connection between quantum gravity and seemingly disparate condensed matter systems demands a relentless focus on mathematical rigor. The current landscape, while suggestive, is littered with effective descriptions. True progress lies not in generating more such descriptions, but in uncovering the fundamental principles that necessitate them.

Original article: https://arxiv.org/pdf/2602.12339.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Emergence of Complexity: Beyond Traditional Quantum Systems

Non-Perturbative Approaches: Solving the Intractable

Quantifying Entanglement: Unveiling the Quantum Nature

From Quantum System to Gravity: A Spacetime Emergence

Beyond the Looking-Glass

See also: