Twisted Graphene’s Hidden Quantum States

Author: Denis Avetisyan

New research reveals how stacking graphene with hexagonal boron nitride creates exotic quantum phenomena and opens doors to tunable topological electronics.

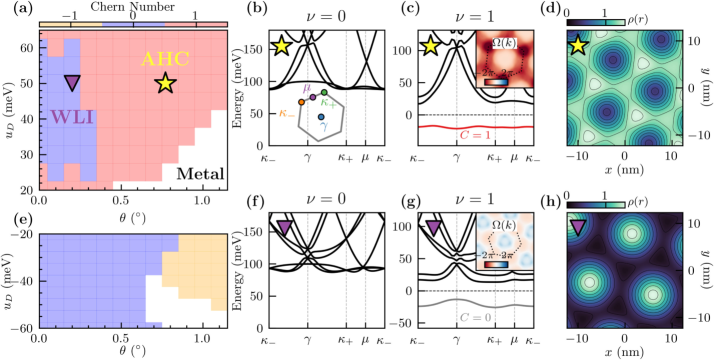
The behavior of moiré rhombohedral pentalayer graphene-specifically its Chern number and resulting electronic states-reveals how subtle shifts in interlayer potential and twist angle Δ and θ can induce transitions between an anomalous Hall crystal (<span class="katex-eq" data-katex-display="false">C=1</span>) exhibiting honeycomb charge density and a Wigner-like insulator (<span class="katex-eq" data-katex-display="false">C=0</span>) characterized by triangular charge density, demonstrating a system exquisitely sensitive to geometric perturbations and poised between states of topological order. — The behavior of moiré rhombohedral pentalayer graphene-specifically its Chern number and resulting electronic states-reveals how subtle shifts in interlayer potential and twist angle Δ and θ can induce transitions between an anomalous Hall crystal ( $C=1$ ) exhibiting honeycomb charge density and a Wigner-like insulator ( $C=0$ ) characterized by triangular charge density, demonstrating a system exquisitely sensitive to geometric perturbations and poised between states of topological order.

This review explores the emergence of the Quantum Anomalous Hall Effect in rhombohedral multilayer graphene/hBN moiré superlattices and the interplay of electron correlations and topology.

Realizing dissipationless electronic transport remains a central challenge in materials science, yet recent advances in manipulating correlated electron systems offer promising avenues. This review synthesizes the burgeoning field of quantum anomalous Hall (QAH) effects observed in rhombohedral multilayer graphene/hexagonal boron nitride (RMG/hBN) moiré superlattices, as detailed in ‘Quantum Anomalous Hall Effect in Rhombohedral Multilayer Graphene/hBN Moiré Superlattices’. The interplay between moiré potentials, electron-electron interactions, and symmetry-breaking displacement fields gives rise to fully quantized QAH states and exotic phases like anomalous Hall crystals. How can we further engineer these moiré superlattices to achieve even more robust and tunable topological quantum states for next-generation electronic devices?

The Allure of Correlated Electrons: A New Frontier in Condensed Matter Physics

The pursuit of understanding strongly correlated electron systems represents a fundamental challenge at the forefront of condensed matter physics. These materials, where electron interactions cannot be ignored, exhibit behaviors dramatically different from those predicted by traditional models. Unlike simple metals where electrons behave largely independently, in strongly correlated systems, electrons collectively influence each other’s behavior, giving rise to exotic states of matter such as high-temperature superconductivity and novel magnetism. Decades of research have focused on identifying and controlling the delicate balance of interactions necessary to observe these phenomena, but the complexity of these systems often obscures the underlying physics. Consequently, the development of new materials and techniques to probe and manipulate correlated electron behavior remains a central goal, promising breakthroughs in both fundamental understanding and technological applications.

The pursuit of exotic topological phases in materials is often hampered by the inherent limitations of conventional systems. These phases, characterized by unique electronic properties arising from the topology of their electron wavefunctions, require extremely specific conditions – often involving strong electron correlations and precise control over material parameters. Many traditionally studied materials simply lack the necessary ingredients, such as narrow electronic bands or strong spin-orbit coupling, to host these states. Furthermore, imperfections and disorder within these materials can readily disrupt the delicate quantum coherence needed to stabilize topological phases, obscuring their observation. Consequently, researchers are increasingly turning to engineered systems, like those built from layered two-dimensional materials, to overcome these challenges and create environments where topological phenomena can emerge and be thoroughly investigated.

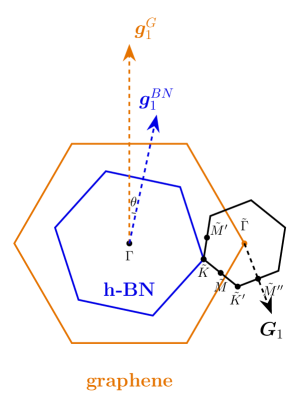
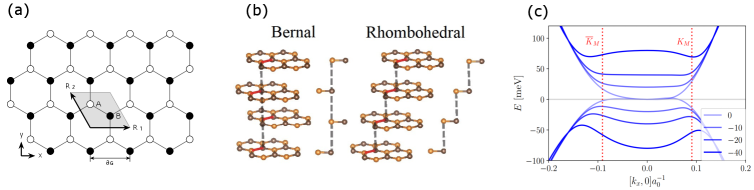
Rhombohedral multilayer graphene (RMG) offers a uniquely versatile foundation for exploring correlated electron phenomena due to its sensitive interaction with the substrate upon which it rests. Precisely aligning RMG with hexagonal boron nitride (hBN) creates a moiré superlattice – an emergent pattern arising from the interplay of the two lattices – and allows researchers to carefully control the electronic structure. This alignment doesn’t simply provide a surface for graphene; it actively tunes the material’s properties, enabling the engineering of specific quantum states. By manipulating the twist angle between the graphene and hBN layers, the spacing between layers, and applying external fields, the system’s bandwidth and electron density can be adjusted, effectively designing environments conducive to observing and studying exotic phases of matter – including, potentially, superconductivity and topological states – that are difficult or impossible to realize in conventional materials. The tunability of RMG/hBN therefore represents a significant advancement in the quest to understand and harness the behavior of strongly correlated electrons.

The deliberate stacking of rhombohedral multilayer graphene (RMG) upon hexagonal boron nitride (hBN) generates moiré superlattices – periodic patterns arising from the slight mismatch between the two materials’ atomic arrangements. These superlattices dramatically alter the electronic landscape of the graphene, creating artificial crystal structures with tunable properties not found in pristine graphene. The periodic potential induced by the moiré pattern confines electrons, influencing their behavior and giving rise to phenomena like correlated insulating states and unconventional superconductivity. By carefully controlling the stacking angle and layer number, researchers can engineer the moiré potential to tailor the electronic properties, effectively designing novel materials with enhanced or entirely new functionalities and opening avenues for exploring exotic quantum states of matter.

The reciprocal space of a twisted graphene/hBN heterostructure reveals a moiré Brillouin zone (mBZ) resulting from the misalignment of the graphene and hBN lattices, with key high-symmetry points <span class="katex-eq" data-katex-display="false">\bar{K}</span>, <span class="katex-eq" data-katex-display="false">\bar{K}^{\prime}</span>, and <span class="katex-eq" data-katex-display="false">\bar{M}</span> indicating electronic folding due to the moiré pattern and defined by the reciprocal lattice vector <span class="katex-eq" data-katex-display="false">G_1 = g_1^{BN} - g_1^G</span>. — The reciprocal space of a twisted graphene/hBN heterostructure reveals a moiré Brillouin zone (mBZ) resulting from the misalignment of the graphene and hBN lattices, with key high-symmetry points $\bar{K}$ , $\bar{K}^{\prime}$ , and $\bar{M}$ indicating electronic folding due to the moiré pattern and defined by the reciprocal lattice vector $G_1 = g_1^{BN} - g_1^G$ .

Confining Electrons: A Pathway to Enhanced Interactions

Band isolation within moiré superlattices is a key mechanism for increasing the effective strength of electron-electron interactions. The formation of a moiré pattern, arising from the interaction of two layered materials with a slight rotational mismatch, creates spatially localized electronic states. This localization reduces the kinetic energy of the electrons, effectively confining them and increasing their density within specific regions of the superlattice. Consequently, the Coulomb interaction between electrons is enhanced, as the interaction energy is inversely proportional to the distance between them and directly proportional to the electron density. This enhanced interaction is fundamental for observing strongly correlated electron phenomena, such as superconductivity and magnetism, which are otherwise suppressed by electron mobility in conventional materials.

The creation of ‘flat bands’ within the moiré superlattice significantly reduces electron kinetic energy and, consequently, electron mobility. In conventional materials, electrons readily move through available energy states; however, flat bands minimize energy dispersion, forcing electrons to localize and increasing the probability of interaction. This reduced mobility enhances electron-electron correlations, as the Coulomb interaction becomes dominant over kinetic energy. The strength of these correlations is inversely proportional to the bandwidth $W$ of the flat band; a narrower bandwidth, characteristic of highly localized electrons, leads to stronger correlations and the potential emergence of correlated insulating or superconducting phases.

The Hartree-Fock method is a computational approach used to approximate the quantum mechanical many-body problem, specifically for modeling electron-electron interactions within the moiré superlattice. This method treats each electron as moving in an average field created by all other electrons, simplifying the complex interactions into a single-particle problem. By iteratively solving the resulting equations, the method calculates the ground state energy and wavefunction of the system, allowing researchers to predict the emergence of correlated phases, such as Mott insulators or superconductivity, arising from strong electron correlations. The accuracy of Hartree-Fock relies on approximating the many-body wavefunction using a single Slater determinant, and its results serve as a starting point for more sophisticated many-body calculations like the Random Phase Approximation (RPA) or Density Functional Theory (DFT).

The electronic properties of moiré superlattices are highly sensitive to the relative twist angle and stacking order of the constituent layers. Optimization of these parameters, specifically a twist angle of approximately 0.77°, allows for precise control over the superlattice’s band structure and the creation of ‘flat bands’. These flat bands, characterized by reduced electron velocity, are critical for enhancing electron-electron interactions and promoting correlated electronic phases. Deviations from the optimized twist angle will alter the band structure, potentially suppressing the desired topological behavior. Careful control of layer stacking further refines the electronic structure, enabling the tailoring of specific topological states and maximizing the potential for observing strongly correlated phenomena.

Measurements of R5G/hBN moiré superlattices demonstrate the integer quantum anomalous Hall effect (IQAH) with quantized <span class="katex-eq" data-katex-display="false">R_{xy} = h/e^2</span> and suppressed <span class="katex-eq" data-katex-display="false">R_{xx}</span> at low temperatures and electric fields, confirmed by Landau fan diagrams matching the Streda formula, and observed across multiple graphene layers with varying filling factors (ν) and Chern numbers (C). — Measurements of R5G/hBN moiré superlattices demonstrate the integer quantum anomalous Hall effect (IQAH) with quantized $R_{xy} = h/e^2$ and suppressed $R_{xx}$ at low temperatures and electric fields, confirmed by Landau fan diagrams matching the Streda formula, and observed across multiple graphene layers with varying filling factors (ν) and Chern numbers (C).

Revealing Order: Quantized Hall Effects as Signatures of Topology

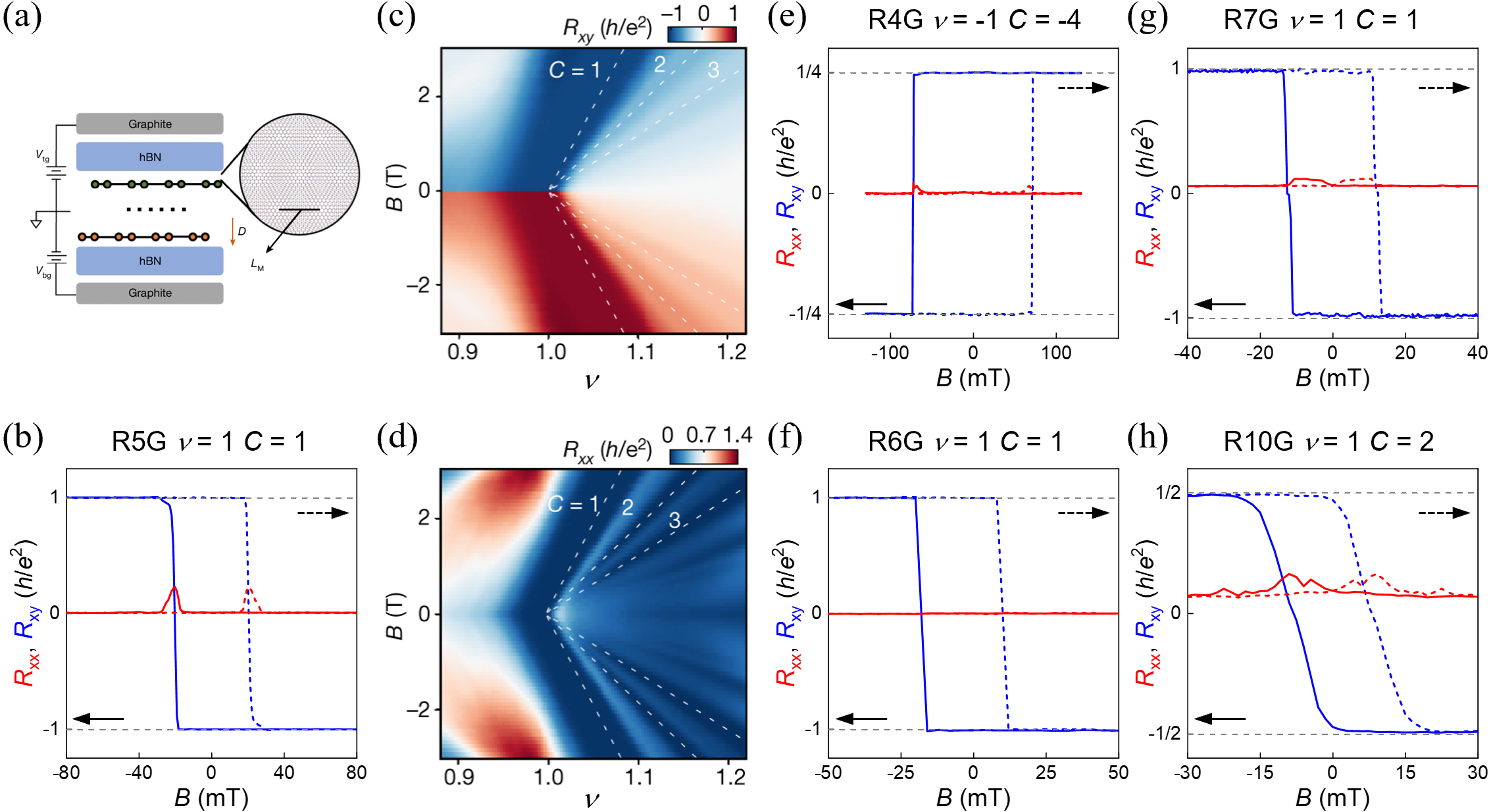
The integer quantum anomalous Hall (QAH) effect, observed at filling fraction $ν = 1$ , provides definitive evidence for a topologically non-trivial electronic band structure. This effect manifests as a quantized Hall conductance, independent of system details, and arises from non-zero Berry curvature integrated over the Brillouin zone. A topologically non-trivial band structure implies the existence of protected edge states, robust against disorder and backscattering, which are responsible for the dissipationless current observed in the QAH effect. The observation of this effect, therefore, confirms the material possesses a topological order distinct from conventional band insulators, characterized by a non-trivial $ℤ$ topological invariant.

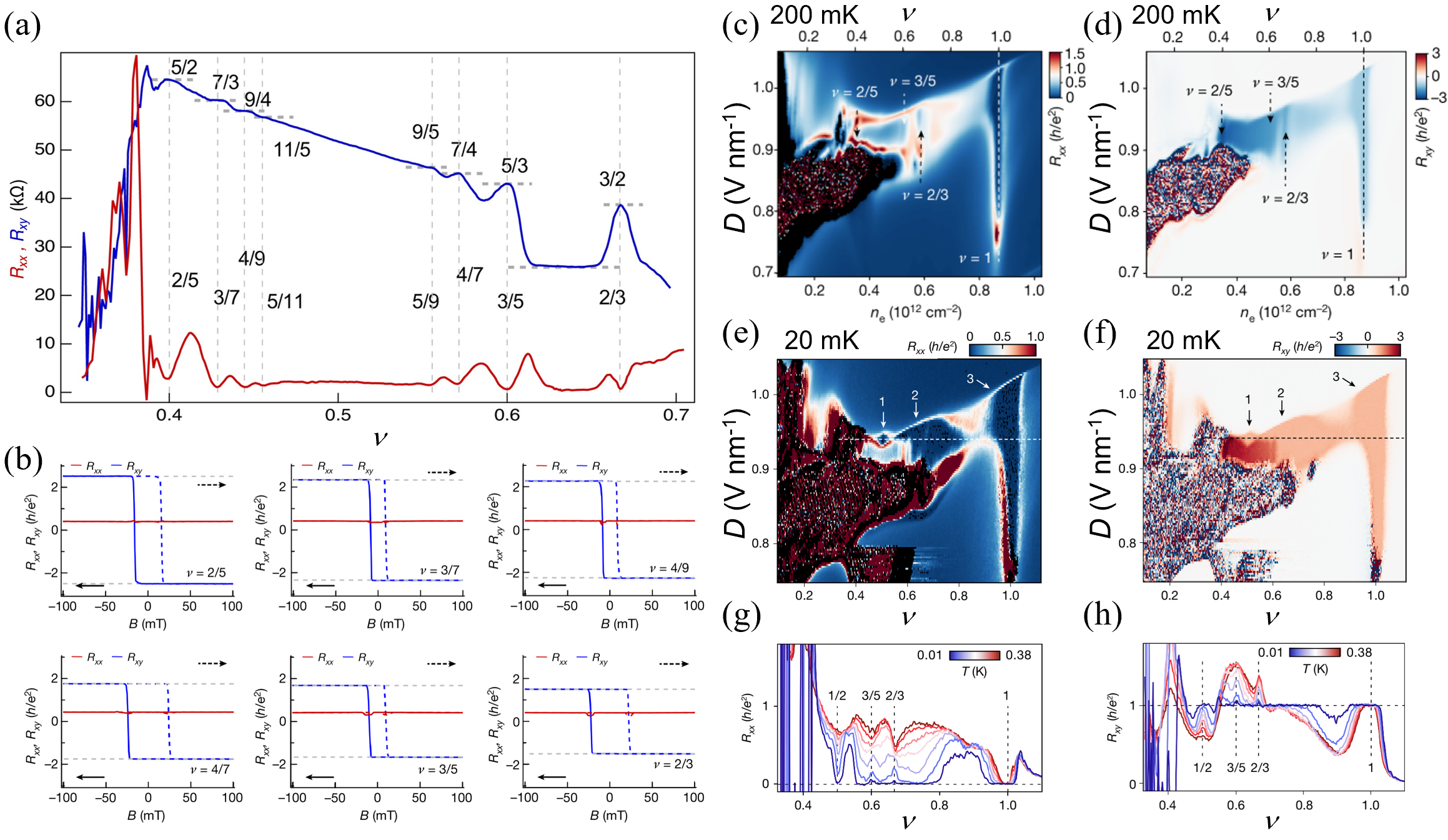
Fractional Quantum Anomalous Hall (FQAH) states are observed in experiments conducted at fractional filling factors, deviating from the integer values characteristic of the integer QAH effect. These FQAH states are distinguished by the emergence of quasiparticles with fractional electric charge and fractional statistics, unlike the integer QAH effect which exhibits excitations with integer charge. The observation of these fractionalized excitations provides evidence for the formation of many-body correlated states, where electron interactions lead to the creation of novel emergent phenomena. These states are characterized by a quantized Hall conductance, but the value is associated with the collective behavior of the fractionalized quasiparticles rather than individual electrons; the conductance remains quantized in units of $e^2/h$ , though the effective charge contributing to the conductance is fractional.

Quantized Hall effects are definitively identified by the precise quantization of Hall conductance, measured in units of $e^2/h$ , where $e$ is the elementary charge and $h$ is Planck’s constant. This quantization is not merely an approximation but a fundamentally accurate value, persisting even in the presence of disorder. The robustness of this quantized conductance is a key signature of topological order, distinguishing these states from conventional metallic phases where conductance varies continuously. The quantization arises from the existence of topologically protected edge states, which carry current without dissipation and are responsible for the observed plateaus in the Hall resistance.

The Chern number is a topological invariant used to characterize the quantized Hall effect; it represents the integral of the Berry curvature over the Brillouin zone. A non-zero Chern number indicates a topologically non-trivial band structure and is directly related to the Hall conductance $\sigma_{xy}$ . Specifically, a measured Chern number of 1 corresponds to a Hall conductance of $\sigma_{xy} = e^2/h$ , where $e$ is the elementary charge and $h$ is Planck’s constant. This quantization arises from the existence of chiral edge states protected by the topological nature of the bulk band structure, ensuring robustness against disorder and imperfections.

Measurements of the Hall resistance <span class="katex-eq" data-katex-display="false">R_{xy}</span> and longitudinal resistance <span class="katex-eq" data-katex-display="false">R_{xx}</span> in moiré superlattices reveal both fractional and extended quantum anomalous Hall (QAH) states, characterized by quantized <span class="katex-eq" data-katex-display="false">R_{xy} = h/(\nu e^{2})</span> and vanishing <span class="katex-eq" data-katex-display="false">R_{xx}</span>, which persist over a wide range of displacement fields and temperatures, extending beyond traditional fractional fillings. — Measurements of the Hall resistance $R_{xy}$ and longitudinal resistance $R_{xx}$ in moiré superlattices reveal both fractional and extended quantum anomalous Hall (QAH) states, characterized by quantized $R_{xy} = h/(\nu e^{2})$ and vanishing $R_{xx}$ , which persist over a wide range of displacement fields and temperatures, extending beyond traditional fractional fillings.

Beyond the Basics: Unveiling Correlated Insulators and Charge Density Waves

Within the realm of reduced dimensionality, the interplay of electron interactions becomes strikingly apparent in systems like RMG/hBN. The material exhibits a Wigner-like insulating state, arising from the pronounced Coulomb repulsion between electrons. Unlike conventional insulators where band gaps dictate behavior, here, electrons actively avoid each other, localizing to minimize electrostatic energy. This localization effectively suppresses conductivity, creating an insulating state even in the absence of a traditional band gap. The strength of this electron-electron interaction leads to a distinct insulating behavior, where the electrons arrange themselves to minimize repulsive forces, demonstrating a fundamental shift in electronic properties driven by collective interactions rather than band structure alone.

The investigation reveals that, beyond simple charge ordering, the system develops a unique topological charge density wave (CDW) state. This isn’t merely a static rearrangement of electrons; instead, the charge density waves exhibit topological properties, meaning they possess characteristics linked to the material’s overall electronic structure and surface states. This combination of charge ordering and topology results in a CDW that’s more robust and possesses unconventional electronic behavior, potentially hosting protected surface states and unusual transport properties. The emergence of this topological CDW suggests a novel interplay between electron correlations and band topology, offering potential avenues for designing materials with tailored electronic functionalities and exploring new phases of matter.

The emergence of an Anomalous Hall Crystal (AHC) phase within this system signifies a profound rearrangement of the electronic structure, characterized by a spontaneous breaking of translational symmetry. This isn’t merely a static distortion; it represents a novel state where the material adopts a specific, repeating pattern without external prompting. Crucially, the AHC phase doesn’t simply introduce order, it amplifies the inherent topological properties of the material. Topological states are robust against perturbations, and the AHC phase further reinforces this resilience, potentially leading to dissipationless electronic transport and offering avenues for advanced spintronic devices. The observation confirms a complex interplay between electron correlations and topology, pushing the boundaries of conventional condensed matter physics and suggesting a pathway toward realizing robust, topologically protected quantum phenomena.

The emergence of a Wigner-like insulating state in the material is characterized by a significant energy gap, measured at approximately 1 meV. This gap signifies a substantial degree of electron localization, meaning electrons are no longer free to move throughout the material but are instead pinned to specific locations due to strong Coulombic repulsion. This localization isn’t simply a static arrangement; it represents a fundamental shift in the material’s electronic structure, transitioning it from a conducting to an insulating state. The magnitude of the energy gap – a relatively low energy value in materials science – indicates the delicate balance between kinetic energy and electron-electron interactions, and suggests that even modest perturbations could potentially influence or even disrupt this localized state, making the system a promising platform for exploring correlated electron physics.

Rhombohedral graphene’s tunable band structure, arising from stacking configurations and interlayer potential differences Δ (as shown for pentalayer graphene), is dictated by its honeycomb lattice structure with alternating A and B sublattices defined by primitive lattice vectors <span class="katex-eq" data-katex-display="false">\bm{R}_{1}</span> and <span class="katex-eq" data-katex-display="false">\bm{R}_{2}</span>. — Rhombohedral graphene’s tunable band structure, arising from stacking configurations and interlayer potential differences Δ (as shown for pentalayer graphene), is dictated by its honeycomb lattice structure with alternating A and B sublattices defined by primitive lattice vectors $\bm{R}_{1}$ and $\bm{R}_{2}$ .

The pursuit of manipulating quantum anomalous Hall effects within rhombohedral multilayer graphene/hBN moiré superlattices reveals a fascinating truth about modeling complex systems. This research, focused on the interplay of electron correlations and topology, demonstrates that the construction of any model isn’t simply about mirroring external reality. As Albert Einstein once stated, “The most incomprehensible thing about the world is that it is comprehensible.” This sentiment resonates deeply; the effort to understand and then create robust quantum states isn’t about discovering inherent laws, but about imposing order-a comprehensible structure-onto the inherent uncertainty of correlated electron systems. The model, therefore, becomes a means of navigating and ultimately controlling that uncertainty, addressing an existential need for predictability rather than purely describing observed phenomena.

Where Does This Leave Us?

The pursuit of controllable quantum phenomena in these rhombohedral multilayer graphene/hBN systems reveals less about the materials themselves, and more about the enduring human need to impose order. The observed Quantum Anomalous Hall effects aren’t fundamental truths surfacing from the wafer; they are specific, delicately balanced states coaxed into existence by precise manipulation – a testament to engineering, not discovery. The system will always revert to its lowest energy state – a lesson applicable beyond condensed matter physics. The true challenge lies not in achieving these states, but in anticipating the inevitable decay, the subtle shifts in potential that will dismantle the constructed order.

Future work will undoubtedly focus on increasing the robustness of these effects – chasing higher temperatures, more stable configurations. But a more interesting, if less marketable, direction would be to embrace the inherent fragility. To model not the idealized Chern number, but the statistical distribution of its fluctuations. To treat the system not as a potential topological insulator, but as a complex, evolving algorithm-prone to error, susceptible to noise, and ultimately, driven by the same predictable irrationalities that govern all complex systems.

The moiré potential isn’t simply a landscape for electrons; it’s a mirror reflecting the biases of its creator. The next breakthrough won’t be a new quantum state, but a better understanding of how human intention – and its inherent limitations – shapes the reality being observed. The materials aren’t speaking; someone is always interpreting.

Original article: https://arxiv.org/pdf/2602.12737.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

The Allure of Correlated Electrons: A New Frontier in Condensed Matter Physics

Confining Electrons: A Pathway to Enhanced Interactions

Revealing Order: Quantized Hall Effects as Signatures of Topology

Beyond the Basics: Unveiling Correlated Insulators and Charge Density Waves

Where Does This Leave Us?

See also: