Author: Denis Avetisyan
A new theoretical approach explores how electron interactions drive emergent behavior at the surfaces and interfaces of complex layered materials.
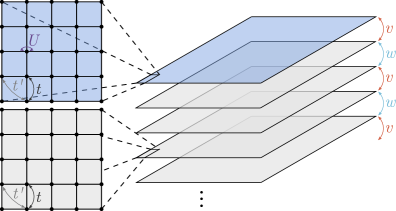
This review details a surface functional renormalization group method applied to the Hubbard-SSH model to investigate correlated phases, including superconductivity and spin-density waves, in layered quantum materials.
Understanding the emergence of correlated electronic states at surfaces and interfaces of layered materials remains a central challenge in condensed matter physics. In this work, ‘Surface Functional Renormalization Group for Layered Quantum Materials’ presents an extension of the functional renormalization group to efficiently address interactions in semi-infinite three-dimensional systems, specifically employing a Hubbard-SSH model to investigate layered structures. We demonstrate that interlayer coupling can induce novel phases, including chiral spin-bond order emerging from a separation of superconducting regimes via incommensurate spin-density wave and spin-bond order. Could this approach unlock a pathway to designing and understanding topological quantum materials with tailored surface properties?
Correlated Electrons and the Quest for Surface Precision
The pursuit of novel materials hinges on a thorough understanding of correlated electron systems, where interactions between electrons dramatically influence material properties. However, conventional theoretical models frequently struggle to accurately depict these systems, particularly when considering surfaces and reduced dimensionality. These models often treat electrons as independent particles, neglecting the crucial many-body effects that emerge from electron-electron interactions. Surface effects exacerbate these limitations, as the broken symmetry and altered electronic structure at a surface introduce complexities not captured by bulk-focused approaches. Consequently, a theoretical framework capable of addressing both strong correlations and surface phenomena is essential for predicting and designing materials with tailored functionalities, paving the way for advancements in fields like superconductivity and quantum computing.
The Hubbard-SSH model emerges as a particularly effective tool for investigating the complex behavior of electrons at material surfaces, where dimensionality is significantly reduced and interactions become paramount. This model uniquely combines the Hubbard interaction – representing the on-site Coulomb repulsion between electrons – with the Su-Schrieffer-Heeger (SSH) model, which describes electron localization driven by variations in hopping integrals along a one-dimensional chain. By integrating these concepts, the Hubbard-SSH model accurately depicts how electron correlations and reduced dimensionality synergistically influence electronic properties. It allows researchers to move beyond traditional approaches and explore phenomena such as metal-insulator transitions, topological phases, and the emergence of localized surface states – all crucial for understanding and ultimately designing novel materials with tailored functionalities. The model’s ability to capture these intricate relationships makes it indispensable for studying correlated electron systems at interfaces and surfaces.
The behavior of strongly correlated electron systems, particularly at surfaces, is acutely sensitive to subtle adjustments in key model parameters. The Hubbard-SSH model captures this sensitivity by explicitly including next-nearest neighbor hopping – representing the ability of electrons to move beyond immediate neighbors – and the chemical potential, which effectively controls the electron density within the system. Altering these parameters fundamentally reshapes the electronic landscape; increasing next-nearest neighbor hopping, for example, can promote the formation of unconventional phases, while manipulating the chemical potential allows for precise tuning of the system’s filling and, consequently, its magnetic and insulating properties. These interactions, combined with the on-site Coulomb repulsion U, dictate the delicate balance between kinetic and potential energies, influencing whether the system favors metallic conductivity, magnetic order, or an insulating state.
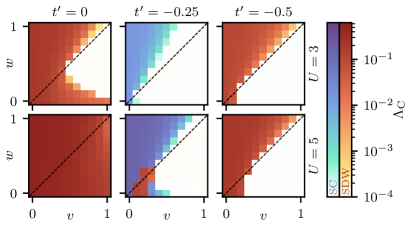
The electronic behavior of correlated materials at surfaces is profoundly influenced by a delicate interplay of parameters within the Hubbard-SSH model, particularly the on-site Coulomb interaction U, alongside hopping integrals and chemical potential. Investigations reveal that the strength of this Coulomb interaction, U, dramatically reshapes the electronic landscape, dictating the system’s susceptibility to hosting exotic phases such as charge density waves or topological states. Specifically, calculations focused on interaction strengths of U = 3 and 5 demonstrate a clear evolution in the electronic structure, leading to localized or delocalized electron behavior and influencing the emergence of these novel phases at the material’s surface. This sensitivity to U highlights the importance of precisely controlling electron correlations to engineer materials with tailored surface properties.
Deciphering Surface Interactions with Functional Renormalization
The Functional Renormalization Group (FRG) is a non-perturbative technique used to analyze many-body systems by systematically integrating out degrees of freedom based on their energy scale; however, applying FRG to surface systems introduces complexities not present in bulk materials. These challenges arise from the reduced dimensionality at the surface, which alters the scaling behavior of interactions and correlation functions. Furthermore, the presence of a bounding surface necessitates careful consideration of boundary conditions and their impact on the flow equations governing the system’s evolution. Standard FRG implementations, designed for translationally invariant bulk systems, require modifications to accurately capture the anisotropy and broken symmetry inherent in surface phenomena. These modifications typically involve incorporating surface-specific terms into the action and adapting the momentum cutoff procedure to reflect the reduced dimensionality.
Surface Functional Renormalization Group (FRG) differs from the standard FRG implementation by directly incorporating the geometric constraints of surface systems. Conventional FRG typically assumes a bulk system with translational symmetry in all directions; however, surfaces exhibit reduced dimensionality and are subject to specific boundary conditions. Surface FRG addresses this by modifying the momentum integration measures and flow equations to reflect the lower-dimensional nature of the surface and the impact of the vacuum-surface interface. This includes adjusting the range of momentum integrals and introducing boundary terms into the effective action to correctly describe surface states and reconstructions. Consequently, the renormalization group flow and resulting phase diagrams obtained through Surface FRG are distinct from those derived using bulk FRG methods, enabling a more accurate description of surface phenomena.
Surface Functional Renormalization Group (FRG) provides a systematic framework for analyzing many-body interactions and correlation effects in surface systems by directly addressing the influence of reduced dimensionality. Unlike mean-field or perturbative approaches which often neglect fluctuations or higher-order correlations, Surface FRG incorporates these effects through the flow equation, allowing for the identification of subtle ordering tendencies. This is achieved by iteratively integrating out high-energy degrees of freedom and renormalizing the interactions, which exposes previously hidden instabilities and phase transitions. Specifically, the method accurately captures the influence of surface-specific interactions and quantum fluctuations on the system’s ground state, revealing ordering patterns that are masked in simpler calculations due to the neglect of these crucial correlation effects.
Surface Functional Renormalization Group (FRG) calculations proceed by systematically eliminating high-energy modes from the system, thereby modifying the effective interactions between the remaining low-energy degrees of freedom. This process is mathematically formalized as a flow equation, typically a set of coupled differential equations, which describe the evolution of the effective action or the interaction vertices as a function of an energy scale Λ. The flow equation details how the interactions are ‘renormalized’ – meaning their strength changes – as the energy scale is lowered from an ultraviolet cutoff to the desired infrared scale. Solving this flow equation provides information about the stability of the system, the emergence of ordered phases, and the critical behavior near phase transitions, offering a non-perturbative approach to understanding the system’s evolution.
Revealing the Emergence of Spin-Density Wave Order
Surface Functional Renormalization Group (FRG) calculations predict the development of spin-density wave (SDW) order within the Hubbard-SSH model when certain parameter conditions are met. The Hubbard-SSH model, a one-dimensional system incorporating both hopping terms and on-site interactions, exhibits a tendency towards SDW formation under appropriate values of interaction strength and hopping parameters. These calculations demonstrate that the system transitions to a phase characterized by spatially modulated spin alignment, indicative of SDW order. The emergence of this order is not guaranteed across all parameter regimes; specific combinations of hopping integrals and interaction strengths are necessary to stabilize the SDW phase, as determined by the FRG flow equations.
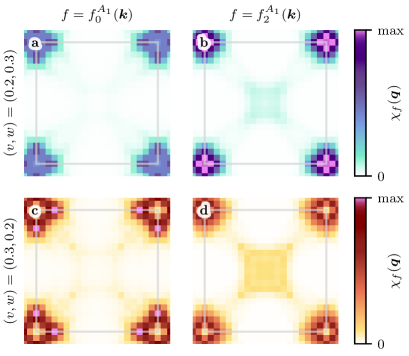
Surface Functional Renormalization Group (FRG) calculations indicate the presence of incommensurate spin-density wave (SDW) order in the Hubbard-SSH model. This order is characterized by a spatial modulation of the spin density with a wavelength that is not commensurate with the underlying lattice spacing; specifically, the period of the SDW is an irrational multiple of the lattice constant. This contrasts with commensurate SDW phases where the wavelength is a simple rational fraction of the lattice spacing. The emergence of incommensurate order is a key finding, as it signifies a more complex spin texture and distinguishes this phase from simpler, commensurate magnetic arrangements.
The stabilization of incommensurate spin-density wave (SDW) order is directly linked to the interplay between the form factor and chiral superposition within the Hubbard-SSH model. The form factor, representing the spatial extent of interactions, modulates the range over which spin couplings are effective, favoring wavevectors that minimize energy. Simultaneously, the chiral superposition-a combination of different spin configurations-introduces a directional preference in the SDW, influencing its wavelength and overall texture. Specifically, constructive interference within the chiral superposition promotes a non-integer relationship between the SDW wavevector and the reciprocal lattice vector, resulting in the observed incommensurability. Alterations to the hopping parameters (v, w) and interaction strength impact both the form factor and chiral superposition, consequently modifying the spin texture and the stability of the incommensurate phase.
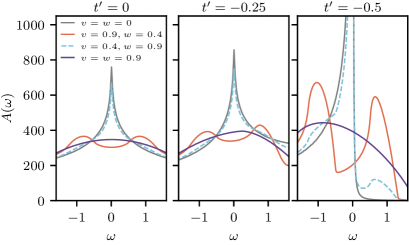
Analysis of the spectral function provides corroborating evidence for the emergence of spin-density wave (SDW) order, displaying features consistent with the predicted phase. Specifically, the spectral function exhibits characteristic signatures related to the formation of the SDW state. The critical scale \Lambda_C , which demarcates the onset of this order, is not fixed but demonstrates a parameter dependence; its value is modulated by alterations in the hopping parameters v and w , as well as the strength of the interaction term within the Hubbard-SSH model. This indicates a tunable transition to the SDW phase controlled by these fundamental system properties.
Expanding Our Understanding and Charting Future Directions
The theoretical prediction of an incommensurate spin-density wave (SDW) order offers a new perspective on the magnetic behavior observed in surfaces and thin films. Conventional understanding often focuses on commensurate magnetic structures, where the magnetic moments align in a simple, periodic pattern; however, this research demonstrates that more complex, incommensurate arrangements – where the periodicity of the magnetic moments doesn’t match the underlying lattice – are not only possible but can significantly influence material properties. This is particularly relevant for nanoscale magnetic systems where surface effects and reduced dimensionality can stabilize these unconventional magnetic phases. Consequently, a greater appreciation for incommensurate SDW order promises to refine models used to predict and control magnetism in these technologically important materials, potentially leading to advancements in data storage and other magnetic devices.
This research establishes a robust theoretical foundation for the rational design of materials exhibiting specific magnetic characteristics, opening avenues for advancements in spintronics. By detailing the intricate relationship between electronic structure and magnetic order, the framework allows researchers to predict and tailor magnetic properties through material composition and structural control. This predictive capability is crucial for developing novel spintronic devices – those leveraging electron spin rather than charge – with enhanced performance and functionality. The ability to engineer materials with precisely controlled magnetic textures promises improvements in data storage, magnetic sensors, and potentially even quantum computing technologies, marking a significant step towards realizing the full potential of spin-based electronics.
Investigations are poised to examine the intricate relationship between spin-density wave (SDW) order and superconductivity within analogous material systems. The co-existence of these two distinct quantum phases-one characterized by a periodic modulation of the spin density and the other by the dissipationless flow of electrical current-is predicted to yield novel emergent phenomena. Specifically, researchers anticipate that the SDW order could either mediate or suppress superconductivity, depending on the specific material parameters and the coupling strength between the spin and charge degrees of freedom. This pursuit aims to uncover unconventional superconducting mechanisms and potentially engineer materials exhibiting enhanced superconducting properties, opening doors for advancements in energy-efficient technologies and quantum computing.
Further investigations utilizing the Surface Functional Renormalization Group (FRG) approach stand to unveil a richer tapestry of physical phenomena by incorporating additional interacting degrees of freedom. A systematic variation of hopping parameters, specifically v and w ranging from 0 to 1, has already begun to map out the resulting phase diagram, demonstrating sensitivity to subtle changes in system parameters. This detailed exploration suggests the potential for discovering novel correlated electron states and emergent behaviors not captured by simpler models, potentially including unconventional superconductivity or topological phases. By broadening the scope of the FRG to encompass factors like electron-phonon interactions or long-range Coulomb interactions, researchers anticipate a more complete understanding of the complex interplay governing these materials and the potential for designing materials with precisely tailored functionalities.
The study meticulously details how emergent correlated phases arise at surfaces, echoing a fundamental principle of interconnectedness. This mirrors Isaac Newton’s observation, “An object in motion tends to stay in motion.” Just as a physical system’s state is determined by its history, the surface’s correlated behavior – be it a spin-density wave or superconductivity – isn’t isolated. It’s intrinsically linked to the bulk material and the interfacial conditions. The surface functional renormalization group method elegantly captures this holistic behavior, demonstrating that understanding the whole system is paramount, not merely focusing on individual components. Scalability, in this context, isn’t about computational power, but rather the clarity of understanding these complex interdependencies.
Future Directions
The presented surface functional renormalization group approach, while a step toward understanding correlated behavior in layered materials, inevitably highlights where the true complexities reside. The method’s efficacy is predicated on a judicious choice of initial conditions and truncation schemes-a familiar constraint. The real challenge isn’t necessarily improving the numerics, but recognizing that the emergent phenomena at surfaces are not simply a redecoration of the bulk. The decoupling of surface and bulk, even within this framework, feels like a convenient fiction, obscuring the subtle feedback loops that govern their interplay.
Future work must address the limitations of static mean-field descriptions. Incorporating dynamical mean-field theory, or exploring non-equilibrium extensions of the FRG, will be essential for capturing the interplay between correlations and kinetic energy. More importantly, the focus should shift from seeking specific correlated phases-superconductivity, spin-density waves-to understanding the principles that govern the emergence of order. Cleverness in proposing new Hamiltonians will yield diminishing returns; simplicity in the underlying description, coupled with a robust methodology, is the more promising path.
Ultimately, the true cost of freedom-the ability to model complex systems-lies in the dependencies introduced by approximations. Each layer of abstraction leaks information, and a complete understanding requires a careful accounting of these losses. The aim should not be to build a perfect model, but a model that reveals its own limitations, guiding the search for a more fundamental description.
Original article: https://arxiv.org/pdf/2601.11055.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Darkwood Trunk Location in Hytale
- How To Watch A Knight Of The Seven Kingdoms Online And Stream The Game Of Thrones Spinoff From Anywhere
- Hytale: Upgrade All Workbenches to Max Level, Materials Guide
- Ashes of Creation Rogue Guide for Beginners
- Best Controller Settings for ARC Raiders
- Olympian Katie Ledecky Details Her Gold Medal-Winning Training Regimen
- Daredevil Is Entering a New Era With a Chilling New Villain (And We Have A First Look) (Exclusive)
- Matt Damon’s Wife Thought Ben Affleck Was the Cute One Before Meeting
- RHOBH’s Jennifer Tilly Reacts to Sutton Stracke “Snapping” at Her
- Travis Kelce Steps Out With Taylor Swift Amid NFL Retirement Rumors
2026-01-20 03:02