When Watching Changes the Game: Quantum Detection and the Observer Effect

Author: Denis Avetisyan

New research reveals how the act of measuring a quantum particle alters the very timing of its first detection, shifting the statistical behavior from predictable to surprisingly complex.

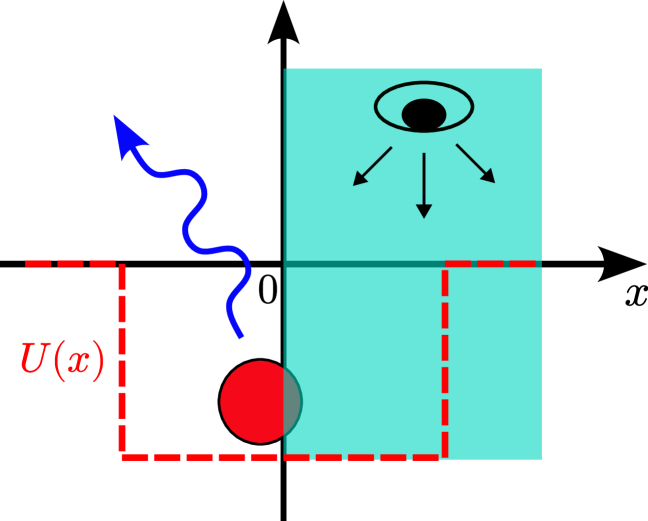
A particle within a potential well undergoes stroboscopic measurement to determine its position, and the energy imparted by this measurement process increases the probability of escape from the well, ultimately causing a shift in the statistical distribution of the time it takes for first detection.

This study demonstrates a measurement-induced crossover in the statistics of first detection times, influenced by the system’s energy spectrum and exhibiting a transition between exponential and algebraic decay.

The conventional understanding of first-detection times diverges in the quantum realm due to the unavoidable influence of measurement itself. This is the central focus of ‘Measurement-induced crossover in quantum first-detection times’, which investigates how repeated quantum measurements alter the statistics of detecting a particle in a target state. The authors demonstrate a crossover from exponential to algebraic decay in first-detection probabilities, dictated by the particle’s energy spectrum and degree of confinement-a purely quantum phenomenon absent in classical first-passage problems. Does this measurement-induced behavior offer a new pathway for controlling and manipulating quantum systems through strategically timed observations?

Beyond Classical Trajectories: Embracing Quantum First Passage

Classical first passage statistics, a cornerstone in modeling the time it takes for a particle to reach a boundary, fundamentally assumes predictable, well-defined trajectories. However, this approach breaks down at the nanoscale, where the principles of quantum mechanics dictate that particles don’t follow singular paths but exist as probability distributions. This means a particle can, in effect, ‘tunnel’ through barriers or explore multiple pathways simultaneously, drastically altering the expected time of first arrival. Consequently, traditional calculations, reliant on deterministic trajectories, fail to accurately capture the behavior of quantum particles, necessitating a new theoretical framework that accounts for the inherent uncertainty and wave-like nature of matter at these diminished scales. The implications of this shift extend to numerous fields, from understanding the rates of chemical reactions to designing more efficient nanoscale electronic devices.

The precise timing of a particle’s initial encounter with a boundary – its first passage time – underpins a surprising range of phenomena across diverse scientific disciplines. In chemistry, this dictates the rates of reactions, determining how quickly molecules combine or decompose. Similarly, in materials science and condensed matter physics, understanding first passage is critical to modeling electron transport, crucial for the development of faster and more efficient electronic devices. Even biological processes, such as the binding of enzymes to substrates or the transmission of signals across neuronal membranes, rely on the fundamental principles governing a particle’s first arrival at a specific location. Therefore, a thorough understanding of this seemingly simple event provides a foundational element for progress in fields ranging from the design of novel catalysts to the development of advanced quantum technologies.

The time it takes a quantum particle to first reach a specific boundary – its first passage time – is significantly altered by the act of continuous measurement, according to recent investigations. Unlike classical predictions which assume a well-defined trajectory, this research demonstrates that persistent observation fundamentally changes the particle’s behavior. The study reveals that continuous measurement introduces a “back action” that steers the particle away from the classically expected path, leading to deviations in the first passage time distribution. Specifically, the findings indicate a crossover from exponential decay – characteristic of classical first passage – to an algebraic decay governed by the strength of the measurement process, highlighting the profound influence of quantum observation on even seemingly simple dynamical events.

This research, bolstered by the PNRR MUR Project, develops a comprehensive theoretical foundation for understanding quantum first passage phenomena – the time it takes a quantum particle to reach a boundary for the first time. The study reveals that continuous quantum measurement significantly alters this timing, causing a notable transition in the decay of first passage times. Specifically, the work demonstrates a shift from the classical expectation of exponential decay – where the probability of first passage decreases rapidly – to algebraic decay, characterized by a slower, power-law decrease. This crossover, driven by the ‘back action’ of the measurement process on the quantum system, has implications for diverse fields where understanding such timing is critical, offering a more accurate prediction of reaction rates and transport properties at the quantum level.

For a particle in a finite-depth potential well, the first-detection probability initially decays exponentially, transitioning to an algebraic decay <span class="katex-eq" data-katex-display="false">F_n \propto n^{\mu}</span> with <span class="katex-eq" data-katex-display="false">\mu \approx 2.8</span> as the average energy becomes positive and the probability of being in a bound state diminishes, as demonstrated by simulations with <span class="katex-eq" data-katex-display="false">a=5.0</span>, <span class="katex-eq" data-katex-display="false">U_0=-2</span>, <span class="katex-eq" data-katex-display="false">x_0=-2</span>, and <span class="katex-eq" data-katex-display="false">\sigma=1</span>. — For a particle in a finite-depth potential well, the first-detection probability initially decays exponentially, transitioning to an algebraic decay $F_n \propto n^{\mu}$ with $\mu \approx 2.8$ as the average energy becomes positive and the probability of being in a bound state diminishes, as demonstrated by simulations with $a=5.0$ , $U_0=-2$ , $x_0=-2$ , and $\sigma=1$ .

The Active Role of Measurement: Shaping Quantum Evolution

Quantum measurement is not a neutral process of simply recording pre-existing properties; it fundamentally alters the state of the measured system. This disturbance, termed ‘measurement back action’, arises from the unavoidable interaction between the measuring apparatus and the quantum system. This interaction introduces correlations, collapsing the system’s wavefunction and forcing it into a definite eigenstate of the measured observable. The degree of disturbance is governed by the uncertainty principle; a precise measurement of one observable necessarily introduces uncertainty in its conjugate variable. Consequently, repeated measurements can significantly influence the system’s temporal evolution, steering it away from the path it would have taken if unobserved. This is distinct from classical measurement, where the observer is assumed to have negligible impact on the observed system.

Stroboscopic measurement involves performing a series of $\text{projective measurements}$ on a quantum system at discrete time intervals. This technique doesn’t provide continuous tracking; instead, each measurement collapses the system’s wave function into a definite state, and the evolution is inferred from the sequence of these collapsed states. The time between measurements is crucial; it dictates the degree to which the system is allowed to evolve between observations, influencing the observed dynamics and allowing for the investigation of phenomena like the quantum Zeno and anti-Zeno effects. Effectively, this repeated measurement acts as a sampling of the system’s state, reconstructing its evolution from a series of snapshots rather than a continuous trajectory.

The Quantum Zeno effect, observed when a quantum system undergoes frequent projective measurements, results in a significant reduction of the system’s evolution rate. This occurs because each measurement collapses the system’s wavefunction into an eigenstate, effectively resetting the evolution and preventing substantial change between measurements. The more frequent the measurements, the shorter the time allowed for evolution, leading to a dramatic slowing or even complete freezing of the particle’s movement. Mathematically, the probability of the particle remaining in its initial state after $n$ measurements approaches 1 as $n$ tends towards infinity, regardless of the underlying time scale for natural evolution. This contrasts with the classical expectation that frequent observation would have a negligible impact on a system’s trajectory.

The Non-Zeno regime describes the behavior of a quantum system when measurements are performed infrequently, allowing substantial temporal evolution between each observation. In this scenario, the probability of finding the system in its initial state decreases more rapidly than predicted by the system’s natural decay rate. This accelerated decay is a direct consequence of the wave function collapsing with each measurement, effectively resetting the evolution timeline and increasing the probability of observing a different state. The observed decay rate is therefore not solely determined by the system’s inherent properties, but is demonstrably influenced by the measurement frequency; lower frequencies result in a faster apparent decay.

The first-detection probability <span class="katex-eq" data-katex-display="false">F_n</span> for a harmonic oscillator varies with the number of measurements <span class="katex-eq" data-katex-display="false">n</span>, exhibiting resonant behavior where it either vanishes at multiples of the period or after the first measurement, and otherwise decays exponentially with a rate of approximately <span class="katex-eq" data-katex-display="false">\alpha \sim eq 2.0</span> as shown for <span class="katex-eq" data-katex-display="false">\omega = 2.45</span>. — The first-detection probability $F_n$ for a harmonic oscillator varies with the number of measurements $n$ , exhibiting resonant behavior where it either vanishes at multiples of the period or after the first measurement, and otherwise decays exponentially with a rate of approximately $\alpha \sim eq 2.0$ as shown for $\omega = 2.45$ .

Mapping Quantum Dynamics: An Analytical Framework

Imaginary potential mapping, employed within the Zeno regime, represents a mathematical technique to address complex quantum time evolution. This involves transforming the original Schrödinger equation, which typically involves a Hermitian Hamiltonian $H$ , into an equivalent problem governed by an imaginary potential $iV(x)$ . This transformation effectively alters the nature of the energy eigenvalues, converting real energies into purely imaginary values. Consequently, the time evolution operator becomes exponentially decaying, simplifying the analysis of quantum dynamics by replacing oscillatory behavior with monotonic decay. This approach is particularly useful for studying systems where frequent measurements inhibit transitions, effectively ‘freezing’ the quantum state and allowing for tractable calculations of the modified dynamics.

Employing imaginary potential mapping facilitates simplification of quantum dynamic calculations by transforming the original time-dependent Schrödinger equation into an equivalent time-independent form. This substitution alters the potential experienced by the quantum particle, effectively changing its energy spectrum and wavefunctions without affecting observable transition probabilities. Consequently, complex temporal evolution becomes solvable through standard eigenvalue problems, reducing computational demands and enabling analytical treatment of systems previously requiring numerical methods. Analysis of the resulting modified dynamics reveals alterations in decay rates and wavefunction behavior, providing insights into the influence of frequent measurements – characteristic of the Zeno regime – on quantum systems.

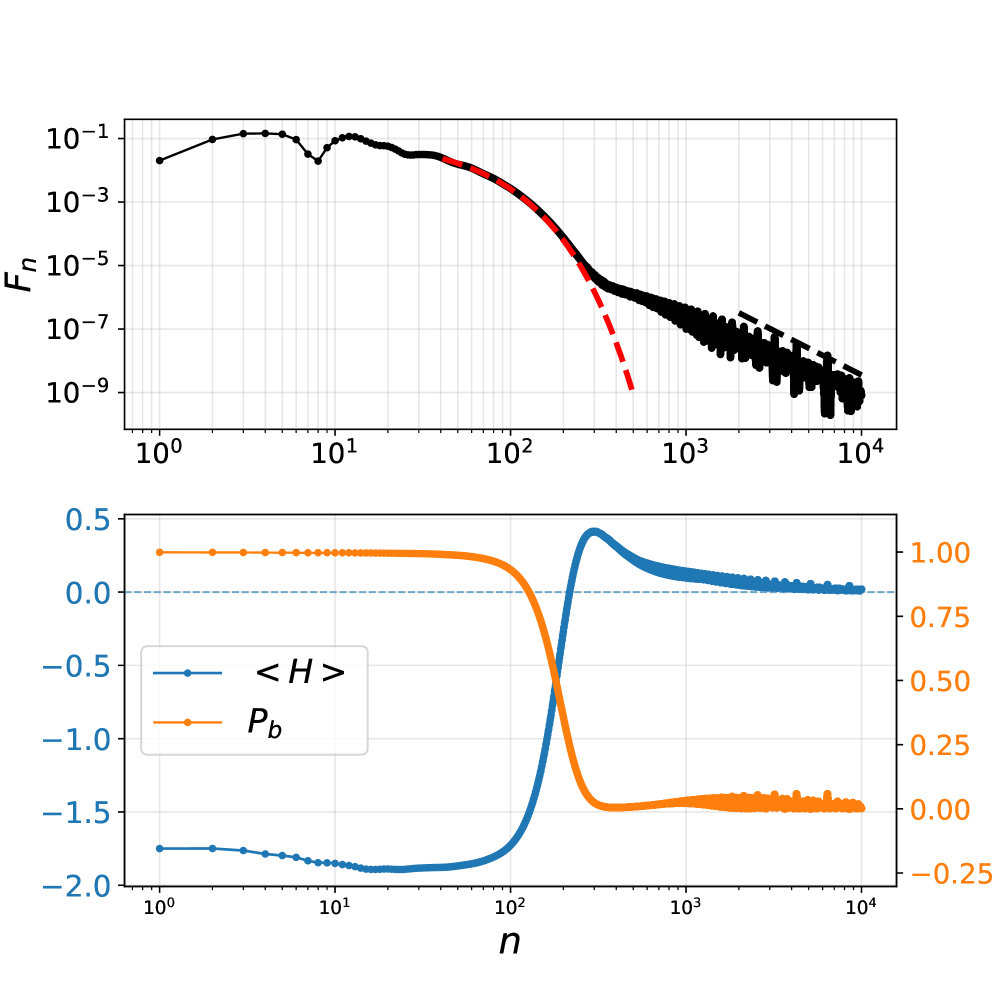
The dynamics resulting from imaginary potential mapping were investigated using three fundamental quantum mechanical model systems: the free particle, the harmonic oscillator, and the infinite potential well. The free particle serves as a baseline for understanding unimpeded propagation. The harmonic oscillator, described by the potential $V(x) = \frac{1}{2}m\omega^2x^2$ , exhibits a discrete energy spectrum and corresponding bound states. Conversely, the infinite potential well, defined by confining potential boundaries, demonstrates a continuous spectrum and scattering states. Analyzing these systems allows for the identification of characteristic behaviors under the transformed dynamics, including the observed transition from exponential to algebraic decay – specifically, an approximate exponent of 2.8 – within the potential well scenario.

Model systems analyzed within the Zeno regime demonstrate spectral characteristics directly correlated to their potential. The harmonic oscillator, possessing a discrete energy spectrum, supports bound states representing quantized energy levels. Conversely, the infinite potential well exhibits a continuous spectrum, giving rise to scattering states and unbound particle behavior. Analysis of the potential well specifically reveals a transition from standard exponential decay of the wave function to algebraic decay, quantified by an approximate exponent of 2.8, indicating a slower rate of particle leakage from the confining potential compared to purely exponential decay scenarios.

The first-detection probability <span class="katex-eq" data-katex-display="false">F_n</span> for a harmonic oscillator exhibits <span class="katex-eq" data-katex-display="false">n^{-3}</span> behavior at low harmonic strengths <span class="katex-eq" data-katex-display="false">ω≲(σ^2τ)^{-1/2}</span>, similar to a free particle, while resonances emerge at <span class="katex-eq" data-katex-display="false">nωτ = κπ</span> with integer κ due to harmonic confinement. — The first-detection probability $F_n$ for a harmonic oscillator exhibits $n^{-3}$ behavior at low harmonic strengths $ω≲(σ^2τ)^{-1/2}$ , similar to a free particle, while resonances emerge at $nωτ = κπ$ with integer κ due to harmonic confinement.

Beyond Exponential Decay: Revealing New Quantum Dynamics

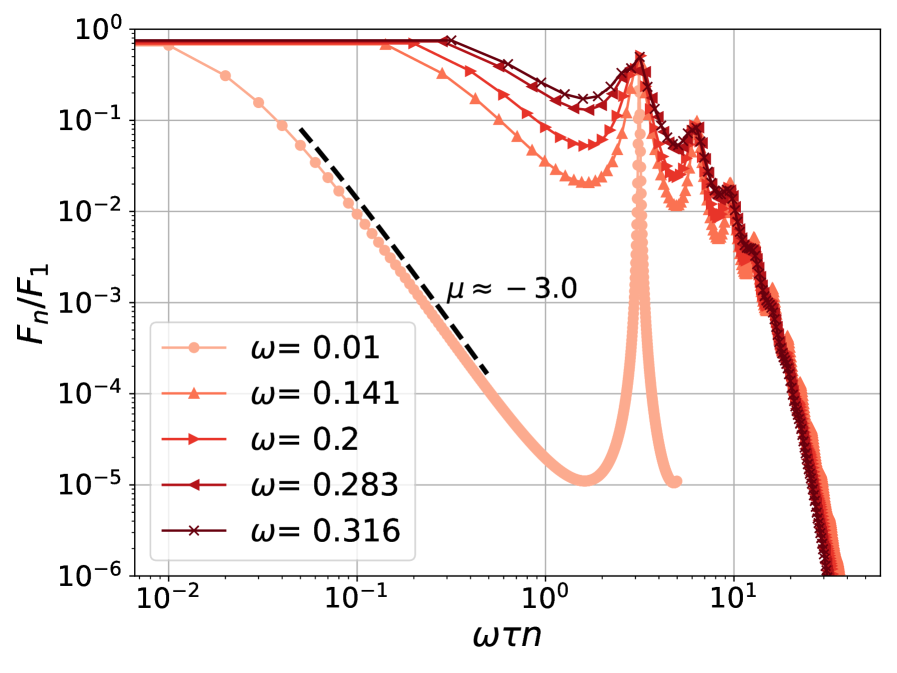
Conventional quantum systems, when unobserved, typically exhibit decay governed by exponential functions – a predictable rate of change over time. However, calculations reveal a stark departure from this classical behavior when subjected to continuous quantum measurement. This ongoing observation doesn’t merely record the system’s evolution; it actively alters it, causing deviations from the familiar exponential decay. Instead of a constant rate, the system’s evolution can follow an algebraic decay, where the probability decreases as a power law – specifically, $n^{-3}$ for a free particle – indicating a significantly slower dissipation. Furthermore, even when an exponential decay persists, its rate is no longer fixed but becomes dependent on the frequency of the measurements themselves, demonstrating that the act of observation fundamentally reshapes the dynamics of the quantum world.

Continuous quantum measurement fundamentally alters the decay of quantum states, moving beyond the predictable exponential decline characteristic of classical physics. Investigations reveal that a free particle, when subjected to ongoing measurement, doesn’t simply diminish; instead, it exhibits an ‘algebraic decay’ – a significantly slower dissipation following a power law with a rate proportional to $n^{-3}$ . This contrasts sharply with the expected behavior and demonstrates the profound influence measurement exerts on quantum evolution. Furthermore, the rate of decay isn’t fixed; it’s dynamically linked to the frequency of measurement, resulting in modified exponential decay rates. These findings highlight that observation isn’t a passive act, but an active intervention that reshapes the timeline of quantum events and offers a pathway to manipulate quantum dynamics.

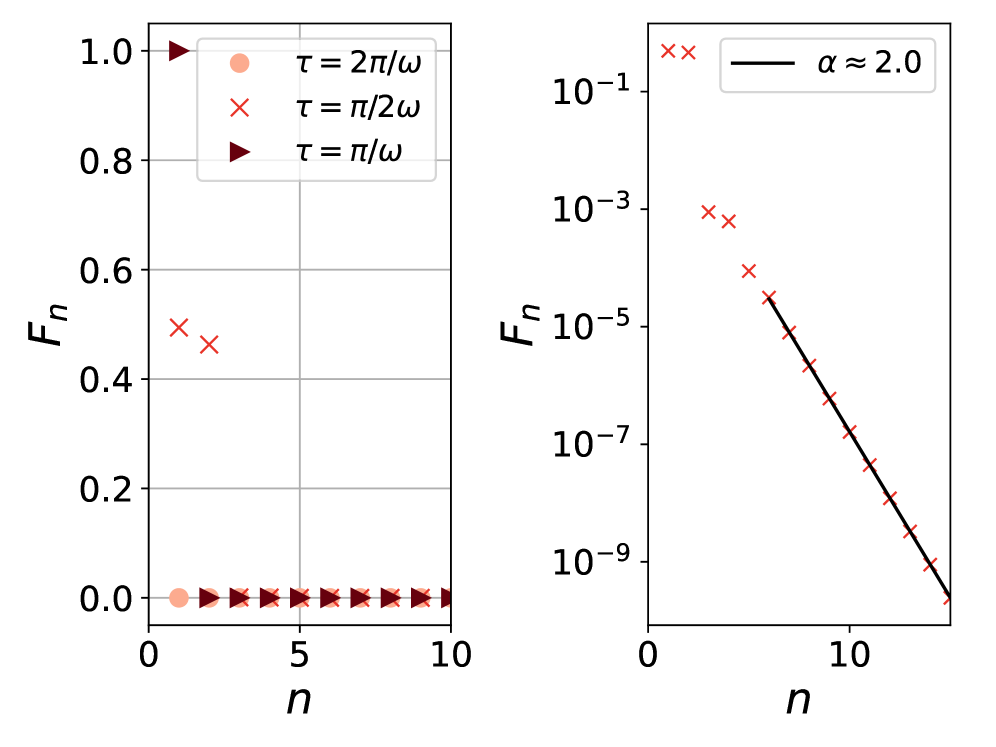
The strength of the potential induced by continuous quantum measurement is demonstrably linked to the duration of the measurement interval. Calculations reveal that this effective measurement potential, denoted as $V_0$ , scales inversely with the measurement time τ, expressed as $V_0 \approx 1/\tau$ . This relationship signifies that shorter measurement intervals induce a stronger effective potential, more significantly perturbing the system’s evolution, while longer intervals exert a weaker influence. Consequently, the ability to control the measurement interval provides a means to tune the strength of this induced potential, effectively shaping the quantum dynamics and offering potential avenues for manipulating quantum states and processes.

Investigations into continuous quantum measurement of the harmonic oscillator reveal specific intervals – $\tau = \pi/\omega$ and its multiples – where detection probability experiences dramatic shifts. These ‘resonant intervals’ arise from the interplay between the measurement process and the natural frequency ω of the oscillator, allowing for unprecedented control over its quantum dynamics. At these intervals, the probability of detecting a particular state can be either maximized, effectively ‘locking’ the oscillator into that state, or minimized, suppressing detection and influencing the system’s evolution. This precise manipulation, achieved solely through the timing of measurements, showcases a pathway to engineer quantum states and control the behavior of quantum systems with remarkable accuracy, potentially impacting fields such as quantum information processing and precision sensing.

The departure from traditional exponential decay, revealed through continuous quantum measurement, carries substantial consequences for interpreting phenomena across diverse quantum systems. Reaction rates, often modeled with simplifying assumptions of immediate decay, may exhibit power-law behavior or modified decay constants influenced by the frequency of environmental interactions-essentially, how often a system is ‘observed’ by its surroundings. Similarly, tunneling-the seemingly impossible passage through energy barriers-is predicted to be sensitive to measurement intervals, potentially altering probabilities and timescales. Crucially, this work offers a framework for modeling quantum dynamics in noisy environments, where constant, unintentional measurement by the environment is unavoidable; understanding these effects is vital for accurately describing everything from chemical reactions to the behavior of quantum devices, moving beyond idealized scenarios toward realistic portrayals of quantum processes.

This investigation establishes a crucial precedent for accurately modeling quantum processes by explicitly accounting for the impact of continuous measurement. Traditionally, quantum dynamics are often simplified by neglecting the disturbance caused by observation; however, this work demonstrates that measurement isn’t merely a passive recording of state, but an active influence on system evolution. By detailing deviations from standard exponential decay – revealing phenomena like algebraic decay and modified decay rates – researchers have moved beyond approximations towards a more nuanced understanding of how observation shapes quantum behavior. The identified relationship between measurement interval and induced potential, $V₀ \approx 1/τ$ , and the resonant behavior of harmonic oscillators provide concrete parameters for incorporating these effects into future theoretical frameworks, ultimately paving the way for more realistic simulations of complex quantum systems in noisy environments and a refined description of fundamental processes like reaction rates and tunneling.

The probability of first detecting a free particle at a position greater than zero decays algebraically with the measurement number <span class="katex-eq" data-katex-display="false">n</span>, exhibiting an effective exponent of approximately -3 regardless of initial conditions or measurement interval [32]. — The probability of first detecting a free particle at a position greater than zero decays algebraically with the measurement number $n$ , exhibiting an effective exponent of approximately -3 regardless of initial conditions or measurement interval [32].

The study illuminates how deeply intertwined observation and reality become at the quantum level. This mirrors the holistic view of systems where altering a single element-in this case, the act of measurement-inevitably ripples through the entire structure. As Niels Bohr stated, “Every atom contains in itself the whole universe.” This principle resonates with the findings, demonstrating that the first detection time isn’t simply a property of the particle but is fundamentally shaped by the measurement process and the energy spectrum of the potential well. The crossover from exponential to algebraic decay isn’t an isolated phenomenon; it’s a consequence of the system’s inherent interconnectedness.

Where Do We Go From Here?

The observation of a measurement-induced crossover in first detection times isn’t merely a curiosity about particle behavior; it’s a signal that the simplest assumptions about quantum systems under interrogation are often flawed. The work highlights a fundamental tension: the very act of seeking information irrevocably alters the system’s evolution. This isn’t about imperfect measurement devices; it’s about the inherent interconnectedness of observation and reality at the quantum level. The energy spectrum, and the degree of confinement, dictate the manner of this alteration – a structural detail with far-reaching implications.

Future investigations must move beyond characterizing this crossover to understanding its broader ecological impact. How does this altered decay influence other quantum processes? Can this measurement-induced shift be harnessed-not to circumvent quantum limits, but to sculpt quantum states in a predictable fashion? The current framework, while illuminating, remains largely confined to idealized potential wells. Extending this analysis to more complex, many-body systems-where interactions create a truly dynamic landscape-will be critical.

Ultimately, the challenge lies in building a more holistic picture. The system isn’t simply a particle in a well, but a node within a network of interactions, constantly shaped by its environment and by the probes that seek to define it. Scalable insights won’t come from increasingly complex models, but from identifying the underlying principles that govern this interplay-the simple rules from which complex behavior emerges.

Original article: https://arxiv.org/pdf/2601.12102.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/

Beyond Classical Trajectories: Embracing Quantum First Passage

The Active Role of Measurement: Shaping Quantum Evolution

Mapping Quantum Dynamics: An Analytical Framework

Beyond Exponential Decay: Revealing New Quantum Dynamics

Where Do We Go From Here?

See also: