Author: Denis Avetisyan
New research reveals that the superradiant phase in the dissipative Quantum Rabi Model isn’t as stable as previously thought, exhibiting a finite lifetime even at large system sizes.
This study demonstrates inherent metastability in the superradiant phase due to spin relaxation within the dissipative Quantum Rabi Model, impacting the long-term behavior of open quantum systems.
While traditionally understood as a stable phase, symmetry-breaking in open quantum systems can be surprisingly fragile. This is explored in ‘Metastability in the Dissipative Quantum Rabi Model’, where we investigate the impact of weak spin relaxation on the superradiant phase. Our analysis reveals that even minimal dissipation renders the superradiant state metastable, characterized by a finite lifetime due to probabilistic decay towards symmetry-preserving states. Does this inherent instability represent a fundamental distinction between steady-state and equilibrium phase transitions in driven-dissipative systems, and what broader implications does it hold for designing robust quantum technologies?
Beyond Idealization: Embracing Dissipation in Quantum Dynamics
The Quantum Rabi Model, a cornerstone in quantum optics, traditionally describes the interaction between a two-level system and a single mode of the electromagnetic field under idealized conditions. However, this foundational model operates on the assumption of a closed system-one entirely isolated from its surroundings. In reality, all quantum systems inevitably interact with their environment, experiencing energy loss through dissipation and a loss of quantum coherence known as decoherence. This interaction fundamentally alters the system’s dynamics, leading to behaviors not predicted by the standard Rabi Model. Consequently, the idealized framework struggles to accurately represent the complex evolution of real-world quantum devices, particularly those designed for applications in quantum technologies where environmental influences are significant. The model’s inability to account for these open-system effects limits its utility in describing processes such as spontaneous emission, energy transfer, and the behavior of quantum circuits.
Quantum systems, unlike idealized theoretical constructs, are never truly isolated. Interactions with surrounding environments – a process known as dissipation – inevitably introduce energy loss and decoherence, fundamentally altering their behavior. This constant exchange of energy and information means that a quantum system’s evolution isn’t solely dictated by its internal Hamiltonian, but also by its coupling to external reservoirs. Consequently, the pristine quantum states described by superposition and entanglement are fragile, tending toward mixed states and classical behavior over time. Recognizing this inherent openness is crucial; models that ignore dissipation provide an incomplete, and often inaccurate, picture of real-world quantum phenomena, from the operation of quantum technologies to the dynamics of molecular interactions and even the early universe. The resulting loss of quantum information necessitates the development of theoretical frameworks capable of accurately capturing these environmental effects and predicting the evolution of open quantum systems.
The Dissipative Quantum Rabi Model represents a significant advancement in understanding quantum dynamics by moving beyond the idealized, closed-system assumptions of its predecessor. While the standard Quantum Rabi Model elegantly describes the interaction between a two-level system and a single mode of the electromagnetic field, it lacks the capacity to account for the inevitable interactions with an environment – a critical limitation for real-world applications. This extended model incorporates dissipation and decoherence, allowing researchers to explore the rich physics of non-equilibrium states and transient behaviors. By introducing terms that describe the loss of energy to the environment, the Dissipative Quantum Rabi Model provides a more realistic framework for investigating phenomena such as spontaneous emission, laser dynamics, and the behavior of quantum systems in noisy environments, ultimately bridging the gap between theoretical predictions and experimental observations. The inclusion of these dissipative terms allows for the study of steady-state properties and the exploration of how quantum coherence is affected by environmental interactions, offering insights into the fundamental limits of quantum technologies.
Unveiling Non-Equilibrium Transitions and Metastability
The Dissipative Quantum Rabi Model, describing the interaction between a single mode of the electromagnetic field and a two-level atom subject to dissipation, undergoes phase transitions fundamentally different from those observed in closed, equilibrium systems. These transitions are driven not by changes in a control parameter affecting the energy spectrum, but by alterations in the balance between coherent system dynamics and irreversible energy loss to the environment. Unlike equilibrium phase transitions characterized by symmetry breaking and diverging correlation lengths, dissipative phase transitions are marked by changes in the system’s steady-state properties and the emergence or disappearance of bistability. Specifically, the rate of energy exchange with the environment-characterized by dissipation parameters like decay rates-directly influences the critical points and the nature of the resulting phases, leading to phenomena such as the transition from a photon-blocked to a photon-emitted state as dissipation increases, which are not present in the standard, lossless Quantum Rabi Model.
Dissipative phase transitions in the Dissipative Quantum Rabi Model can result in metastable states, representing temporary stability not found in equilibrium systems. These states are characterized by a finite lifetime, after which the system will ultimately decay to a lower energy configuration. The duration of this stability is determined by the rate of energy dissipation and the potential energy barrier separating the metastable state from the stable ground state. Unlike true equilibrium states, metastable states are not globally minimal in energy; their apparent stability arises from kinetic limitations preventing immediate relaxation to the true ground state. The system remains in the metastable configuration for a measurable, but limited, time before transitioning due to external perturbations or inherent quantum fluctuations.
The stability and lifetime of metastable states within the Dissipative Quantum Rabi Model are determined by a complex interaction between dissipation and the system’s natural oscillatory behavior. Dissipation, representing energy loss to the environment, introduces a damping effect that reduces the amplitude of these oscillations over time. Simultaneously, the system’s inherent dynamics, characterized by the coupling strength and frequency detuning, dictate the rate of these oscillations. A stronger coupling or a larger detuning can lead to longer-lived metastable states, as the system requires more time to lose sufficient energy to decay. Conversely, increased dissipation shortens the lifetime of these states. The balance between these competing effects establishes a region of stability where the system can persist in a metastable configuration for a measurable duration before transitioning to a lower energy state, with the precise lifetime being dependent on the specific parameters governing both the dissipation rate and the system’s internal dynamics.
Decoding Stability Through the Liouvillian Gap
Liouvillian Gap Analysis is a technique used to assess the stability of steady states in the Dissipative Quantum Rabi Model by examining the eigenvalues of the Liouvillian superoperator. The Liouvillian, a superoperator, describes the time evolution of the density matrix and its eigenvalues determine the decay rates of fluctuations around a given steady state. A finite Liouvillian Gap – the difference between the zero and next-to-zero eigenvalue – indicates that the steady state is stable, as any initial perturbation will decay exponentially. Conversely, a closing gap, where eigenvalues approach zero, signals an instability and potential transition to another state. This method provides quantitative criteria for stability, allowing for a precise determination of conditions under which a specific steady state persists within the model, even in the presence of dissipation and driving fields.
The stability of steady states in the Dissipative Quantum Rabi Model is determined by analyzing the eigenvalues of the Liouvillian superoperator, $L$. A steady state is considered stable if all eigenvalues of $L$ have negative real parts, indicating that the system will return to the steady state after a small perturbation. Conversely, the presence of one or more eigenvalues with positive real parts signifies instability, meaning the system will diverge from the steady state. The magnitude and sign of the real parts of the eigenvalues directly correspond to the rate of approach or departure from the steady state, providing a quantitative measure of stability. Therefore, calculating the eigenvalues of the Liouvillian is crucial for characterizing the dynamic behavior and identifying potential instabilities within the system.
Analysis of the Dissipative Quantum Rabi Model demonstrates that the Liouvillian Gap, denoted as $Δ$, remains finite even as the system size approaches the thermodynamic limit. Specifically, the calculated value of $Δ$ is 0.0034ω₀, where ω₀ represents the characteristic frequency of the system. This persistence of a finite Liouvillian Gap is a key indicator of the metastable nature of the superradiant phase; a closing gap would signify a transition to a stable state. The observed gap size suggests that, while the superradiant phase is not absolutely stable, it exhibits a significant lifetime due to this energetic barrier to decay.
The persistence of a finite Liouvillian gap, measured at 0.0034ω₀, is directly attributable to the weak spin relaxation rate within the Dissipative Quantum Rabi Model. Many open quantum systems demonstrate a closing of this spectral gap following a power-law dependence on system size or relaxation strength, indicating eventual instability. However, our findings demonstrate that even in the thermodynamic limit, the gap remains finite due to the comparatively low rate of spin relaxation, thereby confirming the metastable nature of the superradiant phase and preventing the system from rapidly decaying to its ground state. This contrasts with systems where stronger relaxation mechanisms would drive the gap to zero, inducing instability.
Finite-Size Scaling (FSS) is a crucial analytical approach when investigating the Dissipative Quantum Rabi Model in the thermodynamic limit, where system size approaches infinity. Direct numerical calculations become computationally intractable at such scales; FSS allows for the extrapolation of results obtained from finite-sized systems to predict the behavior of the infinite system. This involves analyzing how key observables, such as the Liouvillian gap $Δ$, scale with system size, typically represented by the number of spins, $N$. By fitting the data to a power law, $Δ \propto N^{-α}$, the critical exponent $α$ can be determined, allowing for accurate prediction of the gap’s value, and therefore stability, as $N$ approaches infinity. The application of FSS ensures reliable analysis of the system’s long-term behavior and confirms the metastable nature of the superradiant phase even in the thermodynamic limit.
Verifying Dynamics and Refining Simulations
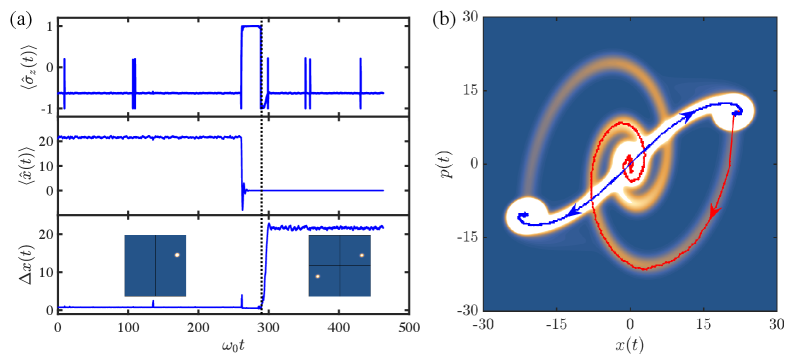
Quantum Trajectory Simulation, applied to the Dissipative Quantum Rabi Model, utilizes a stochastic wavefunction approach to model the time-dependent behavior of quantum states. This method involves solving the Lindblad master equation, which describes the open quantum system’s evolution subject to dissipation and decoherence, by simulating numerous individual quantum trajectories or “realizations”. Each trajectory represents a possible path the system can take, weighted by the probability of that path occurring. By averaging over a large ensemble of these trajectories, the average quantum state and its properties, such as expectation values and purity, can be accurately determined as a function of time. This allows for direct observation of the system’s dynamics, including phenomena like Rabi oscillations, collapses, and revivals, under the influence of dissipation without requiring approximations often found in other analytical or numerical methods.
Cumulant expansion enhances the accuracy of quantum trajectory simulations by systematically including higher-order correlations beyond the mean-field approximation. Standard quantum trajectory methods often truncate correlations after the first order, leading to inaccuracies, particularly in strongly correlated systems. Cumulant expansion provides a perturbative approach to approximate the influence of these higher-order correlations on the system’s evolution. Specifically, it involves expanding the system’s master equation in terms of cumulant operators, which describe the deviations from the mean field. By including terms up to a certain order in the cumulant expansion-typically second or third order-the simulation more accurately captures the complex interactions and correlations within the dissipative quantum Rabi model, resulting in improved fidelity and a more reliable representation of the system’s dynamics. This is achieved without the computational cost of directly simulating the full density matrix.
The Husimi Q representation is employed as a phase-space representation of the quantum state, providing a visualization of the probability distribution over quasi-probabilities. This technique maps the density matrix, $ \rho $, onto a continuous function, Q(α, α), where α represents a complex coordinate in phase space. By examining the time evolution of Q(α, α), one can qualitatively and quantitatively assess the dynamics of the dissipative quantum Rabi model, including the localization and spreading of the wavefunction. The resulting phase-space distributions offer insights into the coherence and decoherence processes, revealing how the quantum state evolves under dissipation and coupling to the environment, complementing the quantitative data obtained from lifetime measurements and principal component analysis.
Analysis of the Dissipative Quantum Rabi Model yielded a characteristic lifetime of $T_m = 294.1\omega_0^{-1}$. This value was determined through quantum trajectory simulations and corroborated by independent principal component analysis of the system’s dynamics. The consistency between these two distinct computational approaches validates the obtained result and provides confidence in the calculated timescale for the decay of the quantum state. The parameter $\omega_0$ represents the fundamental frequency of the system, and its inverse serves as the unit for measuring time in this context.
The Interplay of Symmetry, Relaxation, and Control
The Dissipative Quantum Rabi Model exhibits a fascinating property known as parity symmetry, which profoundly shapes its behavior. This symmetry dictates that the system’s quantum state can be either even or odd under particle number conservation, effectively restricting the possible pathways of its evolution. Consequently, the system’s dynamics are not free to explore all possible configurations, leading to unique and predictable patterns. More importantly, parity symmetry directly influences the nature of the phase transitions the model undergoes; these transitions, shifts in the system’s collective behavior, manifest differently due to the constraints imposed by the symmetry. Specifically, the symmetry can give rise to distinct phases characterized by different levels of quantum coherence and entanglement, and alters the critical points at which these transitions occur, offering a powerful tool for manipulating and controlling quantum systems.
Spin relaxation, a pervasive process in quantum systems, fundamentally alters the behavior of qubits through interactions with their surrounding environment. This interaction doesn’t simply add noise; it actively reshapes the energy landscape, effectively smoothing out the sharp distinctions between quantum states and causing them to lose their superposition. The consequence is decoherence – the gradual loss of quantum information as the system transitions from a purely quantum state to a classical mixture. The rate of spin relaxation is determined by the strength of the coupling to the environment and the density of states available for energy dissipation. Consequently, controlling this relaxation – through careful isolation or engineered dissipation – is crucial for maintaining coherence and enabling reliable quantum computation and sensing; understanding its mechanisms allows for the development of strategies to mitigate its effects and prolong the lifespan of fragile quantum states.
The capacity to precisely control quantum systems hinges on a nuanced comprehension of how symmetry, relaxation, and dissipation interact. While symmetry dictates the allowed states and transitions within a quantum system, dissipation-the loss of energy to the environment-and relaxation-the return to equilibrium-inevitably introduce decoherence and alter the system’s behavior. These competing processes aren’t simply disruptive forces; instead, they present opportunities for steering quantum dynamics. Researchers are discovering that carefully engineered dissipation and relaxation channels, informed by the system’s underlying symmetries, can be harnessed to create specific quantum states, enhance coherence, and even protect quantum information from environmental noise. This interplay is particularly relevant in areas like quantum computing and sensing, where maintaining fragile quantum states is paramount, and the ability to tailor these interactions promises to unlock new levels of control and functionality in future quantum technologies.
The study meticulously dissects the superradiant phase, revealing its inherent instability-a fragility stemming from spin relaxation. It’s a demonstration of how even seemingly robust quantum states can be transient, governed by underlying decay mechanisms. This resonates with a sentiment expressed by Richard Feynman: “The first principle is that you must not fool yourself – and you are the easiest person to fool.” The pursuit of understanding, as evidenced by the paper’s exploration of the Liouvillian gap and cumulant expansion, demands relentless self-scrutiny, acknowledging that appearances can be deceiving and metastable states, however brilliant, are not immune to the laws of decay.
What Lies Ahead?
The demonstration of inherent metastability within the dissipative Quantum Rabi Model is not a conclusion, but a sharpening of the question. The pursuit of a truly stable superradiant phase, even in principle, appears increasingly… optimistic. Further work must address the precise mechanisms by which spin relaxation, and other unavoidable environmental interactions, dictate the ultimate decay. The Liouvillian gap, so elegantly exposed here, is not merely a mathematical curiosity; it is the very boundary between idealized physics and the relentless march toward thermal equilibrium.
Future investigations should not be constrained by attempts to avoid dissipation, but rather to characterize its influence with greater precision. Cumulant expansions offer a path, but they are, by their nature, approximations. A more complete understanding may require venturing beyond perturbative approaches, embracing techniques that directly confront the non-equilibrium dynamics of open quantum systems. Intuition suggests that the observed metastability is a general feature of systems driven far from equilibrium, and establishing this generality would be a valuable, if humbling, achievement.
The pursuit of perfection in quantum control is admirable, but perhaps misguided. A deeper appreciation for the limitations imposed by decoherence-for the inherent fragility of quantum states-may ultimately prove more fruitful than endless attempts to circumvent them. The code of reality, it seems, is written not in pure quantum coherence, but in the messy, irreversible language of thermodynamics.
Original article: https://arxiv.org/pdf/2511.21508.pdf
Contact the author: https://www.linkedin.com/in/avetisyan/
See also:
- Hazbin Hotel season 3 release date speculation and latest news
- 10 Chilling British Horror Miniseries on Streaming That Will Keep You Up All Night
- Dolly Parton Addresses Missing Hall of Fame Event Amid Health Concerns
- The Mound: Omen of Cthulhu is a 4-Player Co-Op Survival Horror Game Inspired by Lovecraft’s Works
- Where Winds Meet: How To Defeat Shadow Puppeteer (Boss Guide)
- 10 Best Demon Slayer Quotes of All Time, Ranked
- Zootopia 2 Reactions Raise Eyebrows as Early Viewers Note “Timely Social Commentary”
- World of Warcraft leads talk to us: Player Housing, Horde vs. Alliance, future classes and specs, player identity, the elusive ‘Xbox version,’ and more
- Victoria Beckham Addresses David Beckham Affair Speculation
- You Won’t Believe What Happens to MYX Finance’s Price – Shocking Insights! 😲
2025-11-29 18:49