Beyond Crystals: Quasicrystalline Phases Emerge in Bose-Bose Mixtures

Author: Denis Avetisyan

New research reveals that aperiodically structured quasicrystalline phases can spontaneously form in binary Bose-Einstein condensates under specific conditions, opening avenues for novel quantum simulations.

A binary Bose-Einstein condensate, subjected to spin-dependent periodic potential and increasing intercomponent interactions <span class="katex-eq" data-katex-display="false">g_{12}</span>, transitions from partially miscible quasicrystalline density clusters exhibiting eightfold rotational symmetry-observed at moderate <span class="katex-eq" data-katex-display="false">g_{12}</span>-to complete phase separation as interactions strengthen, effectively dissolving the delicate order within the system. — A binary Bose-Einstein condensate, subjected to spin-dependent periodic potential and increasing intercomponent interactions $g_{12}$ , transitions from partially miscible quasicrystalline density clusters exhibiting eightfold rotational symmetry-observed at moderate $g_{12}$ -to complete phase separation as interactions strengthen, effectively dissolving the delicate order within the system.

Spin-dependent periodic potentials induce emergent aperiodicity in binary Bose-Einstein condensates through intercomponent interactions, bypassing the need for explicitly aperiodic confinement.

While crystalline order is typically imposed by periodic potentials, the emergence of aperiodicity in quantum systems remains a fascinating challenge. This work, ‘Emergent aperiodicity in Bose-Bose mixtures induced by spin-dependent periodic potentials’, investigates the formation of quasicrystalline phases in binary Bose-Einstein condensates confined by spin-dependent optical lattices. We demonstrate that aperiodically modulated quasicrystalline order can spontaneously arise through the interplay of intercomponent interactions and external potentials, even without explicitly aperiodic confinement. Can this mechanism pave the way for stabilizing and manipulating quantum quasicrystals in broader, experimentally accessible systems?

Beyond the Repeating Pattern: Unveiling Aperiodic Order

Conventional materials, from simple table salt to complex alloys, are fundamentally defined by their periodic atomic arrangements – patterns that repeat in a predictable fashion across the substance. This inherent periodicity, while contributing to material stability, imposes limitations on achievable properties; certain combinations of atoms and desired characteristics simply cannot be realized within a strictly repeating structure. The constraints of periodicity affect a material’s mechanical strength, electrical conductivity, and optical behavior, effectively capping the range of possible functionalities. Scientists theorized that breaking free from this repeating pattern could unlock entirely new material possibilities, and this ultimately led to the discovery of quasicrystals – structures possessing long-range order but lacking the translational symmetry characteristic of traditional crystals, opening a pathway to previously unattainable material properties.

Quasicrystals represent a fascinating departure from traditional crystallography, exhibiting a surprising order without the repeating, translational symmetry found in conventional crystals. This unique arrangement-often described as possessing long-range order but lacking periodicity-gives rise to a host of unusual properties. Unlike crystals which build up from a repeating unit cell, quasicrystals feature patterns that are ordered but do not infinitely repeat, similar to complex geometric tilings. This structural peculiarity translates into exceptional hardness, low friction coefficients, and poor thermal conductivity, making them potentially valuable in applications ranging from protective coatings and thermal barriers to advanced alloys and even data storage. The aperiodic yet ordered nature of quasicrystals allows for tailored electronic and optical characteristics, opening avenues for materials with properties not achievable through conventional crystalline structures.

The synthesis and sustained control of quasicrystalline phases present a formidable hurdle in condensed matter physics, largely due to their inherent instability and sensitivity to even minor perturbations. Unlike crystals, which readily form due to their minimization of energy through periodic arrangements, quasicrystals exist in a precarious balance, demanding exquisitely precise control over temperature, composition, and pressure during their creation. Researchers continually grapple with preventing the system from ‘relaxing’ into a more stable, periodic state, often requiring rapid quenching or specialized alloy compositions to ‘freeze in’ the aperiodic structure. Moreover, characterizing these materials is complex, necessitating advanced diffraction techniques and computational modeling to confirm their long-range order and unravel their unusual physical properties, hindering the development of practical applications that leverage their potential.

The phase diagram of a balanced binary Bose-Einstein condensate, determined by the overlap parameter <span class="katex-eq" data-katex-display="false">\mathcal{O}</span> and parameters <span class="katex-eq" data-katex-display="false">(g_{12}, U)</span>, reveals distinct phases including complete immiscibility, stable and metastable quasicrystalline states exhibiting eightfold symmetry, and a transition from spatial domain formation to complete phase separation. — The phase diagram of a balanced binary Bose-Einstein condensate, determined by the overlap parameter $\mathcal{O}$ and parameters $(g_{12}, U)$ , reveals distinct phases including complete immiscibility, stable and metastable quasicrystalline states exhibiting eightfold symmetry, and a transition from spatial domain formation to complete phase separation.

Confining Chaos: Ultracold Gases as a Quasicrystalline Foundry

Ultracold atomic systems, typically achieved through laser and evaporative cooling to temperatures on the order of nanokelvin, enable unprecedented control over interatomic interactions. This control is realized by tuning external fields – such as magnetic fields for Feshbach resonances – to modify the scattering length and thus the strength and sign of the interactions between atoms. Precise manipulation of these interactions is essential for engineering quasicrystalline order because quasicrystals are stabilized by a delicate balance between short-range bonding and long-range repulsive forces. The ability to finely adjust these forces in ultracold gases allows researchers to move beyond the limitations of material science, where interactions are largely fixed, and explore novel phases of matter exhibiting quasicrystalline symmetry. Furthermore, the weak interactions achievable in these systems minimize heating effects, facilitating the observation of these fragile, non-equilibrium states.

Dipolar quantum gases exhibit anisotropic interactions arising from the electric dipole moments of the constituent atoms. This directionality differentiates them from systems with isotropic interactions, such as those mediated by s-wave scattering, and is key to stabilizing quasicrystalline ground states. Specifically, the long-range and direction-dependent nature of the dipole-dipole interactions can frustrate crystallization into periodic lattices. This frustration promotes the formation of quasicrystalline phases characterized by long-range order without translational symmetry, as the energetic cost of accommodating the dipole orientations can be minimized in non-periodic arrangements. The strength of these dipolar interactions, tunable via magnetic or electric fields, provides a control parameter to navigate the phase diagram and access quasicrystalline states not readily achievable in isotropic systems.

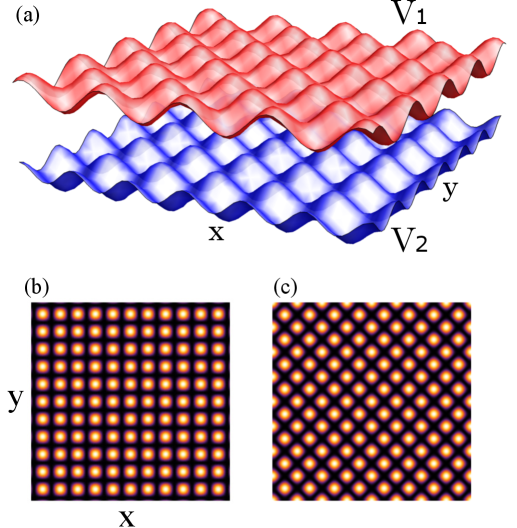
Optical lattices, created by interfering laser beams, serve as a periodic potential for confining ultracold gases. The wavelength of the lasers determines the lattice spacing, and the intensity controls the depth of the potential wells, effectively trapping the atoms at discrete lattice sites. By carefully engineering the lattice geometry – including creating non-periodic or quasiperiodic arrangements – researchers can induce the formation of quasicrystalline structures. These lattices not only provide spatial confinement but also allow for precise manipulation of interatomic interactions through control of lattice parameters and external fields, facilitating the observation and study of quasicrystalline phases in these systems. The use of higher-dimensional lattices, such as three-dimensional cubic or face-centered cubic structures, further expands the possibilities for creating and exploring complex quasicrystalline order.

Independent control of atoms with differing spin states is achieved through the superposition of two perpendicularly oriented, spin-dependent <span class="katex-eq" data-katex-display="false">V_1</span> and <span class="katex-eq" data-katex-display="false">V_2</span> optical lattices. — Independent control of atoms with differing spin states is achieved through the superposition of two perpendicularly oriented, spin-dependent $V_1$ and $V_2$ optical lattices.

Decoding the Whisper: Modeling and Validating Quasicrystalline Phases

The Gross-Pitaevskii equation (GPE) serves as the foundational equation of motion for describing the dynamics of Bose-Einstein condensates (BECs), and its extension to binary BECs allows modeling of systems comprised of two weakly coupled condensate species. The GPE is a mean-field theory derived from the many-body Schrödinger equation, effectively treating the BEC as a single macroscopic wavefunction $\Psi(\mathbf{r}, t)$ . For a binary BEC, two coupled GPEs are utilized, incorporating inter-species interactions alongside intra-species interactions, represented by coupling constants. These equations account for both the kinetic energy of the particles and the mean-field potential arising from the interactions, enabling the prediction of condensate evolution, including phenomena like interference patterns and the formation of spatially ordered structures relevant to quasicrystalline phases.

Path-Integral Monte Carlo (PIMC) simulations have been employed to assess the stability of quasicrystalline phases in systems subject to quantum fluctuations. These simulations, utilizing a many-body approach, calculate the probability of observing a specific configuration of particles based on the system’s Hamiltonian and quantum statistical mechanics. Results indicate that despite the inherent disruptive effects of quantum fluctuations – which introduce uncertainty in particle positions and momenta – stable quasicrystalline order is maintained across a range of parameters. Specifically, the simulations demonstrate the persistence of long-range positional correlations characteristic of quasicrystals, even at finite temperatures, confirming their thermodynamic stability beyond purely classical predictions. The simulations typically involve propagating imaginary-time trajectories of particles, effectively sampling the ground state wavefunction and allowing for the calculation of observables such as the pair distribution function, which reveals the presence and strength of quasicrystalline order.

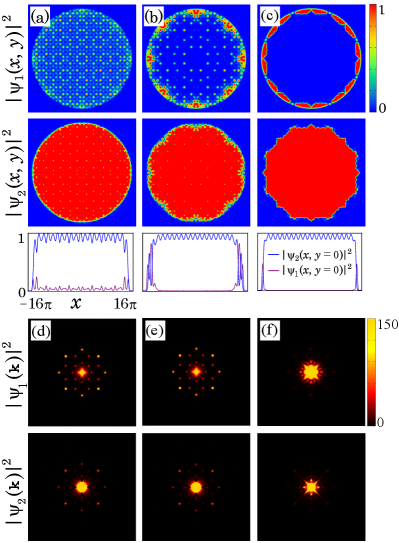
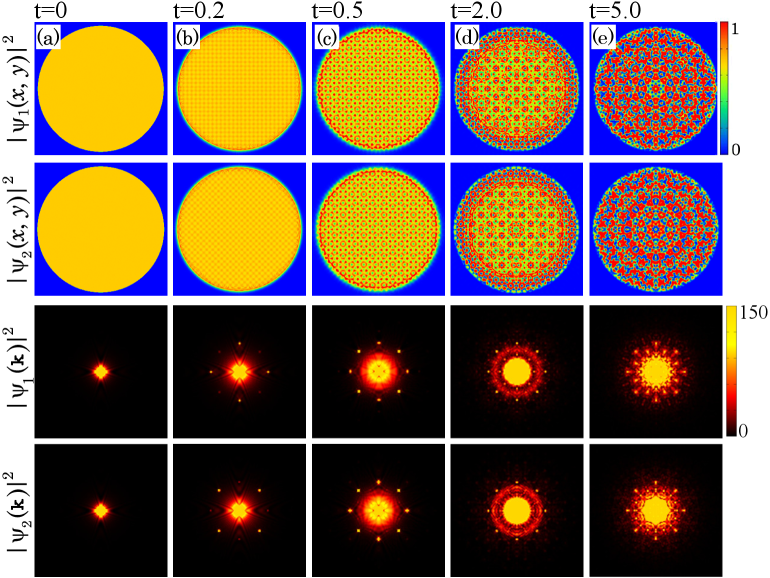
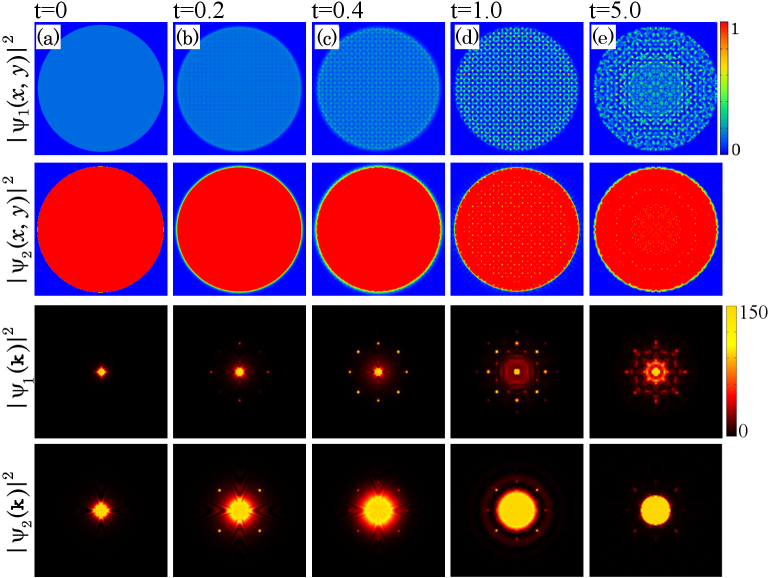
Real-time dynamics simulations have validated theoretical predictions regarding the formation of quasicrystalline phases in Binary Bose-Einstein Condensates. These simulations demonstrate the time-dependent evolution from initial conditions to a stable quasicrystalline state, specifically exhibiting the emergence of eightfold symmetry. The observed symmetry development occurs within a timeframe of 0.2 to 5.0 time units, allowing for direct visualization of the dynamic process and confirmation of the predicted temporal characteristics of quasicrystal formation. The simulations provide quantitative confirmation of the stability and evolution predicted by the underlying theoretical models.

A balanced two-component Bose-Einstein condensate initialized with small random fluctuations in a spin-dependent periodic lattice evolves dynamically, demonstrating stable behavior at an intercomponent interaction strength of <span class="katex-eq" data-katex-display="false">g_{12} = 16.5</span>. — A balanced two-component Bose-Einstein condensate initialized with small random fluctuations in a spin-dependent periodic lattice evolves dynamically, demonstrating stable behavior at an intercomponent interaction strength of $g_{12} = 16.5$ .

Witnessing Emergence: Unveiling the Dance of Order and Disorder

The behavior of a binary Bose-Einstein condensate (BEC) is remarkably sensitive to the interactions between its constituent components. These ‘intercomponent interactions’ don’t simply add to the overall system behavior; instead, they fundamentally reshape the resulting phases and symmetries observed. Strong attractive interactions, for example, can drive the formation of tightly bound molecular states, altering the condensate’s density profile and potentially leading to spatial separation of the two components. Conversely, repulsive interactions promote miscibility and can give rise to intricate, spatially modulated patterns. Importantly, the strength of these interactions acts as a control parameter, effectively ‘tuning’ the system to exhibit different phases – from fully mixed states to phase-separated regimes, and even to exotic states exhibiting unusual symmetries like eight-fold rotational symmetry in the density clusters. Understanding how these interactions influence the collective behavior is therefore crucial for predicting and manipulating the properties of these quantum systems, opening doors to potential applications in precision measurement and quantum information processing.

A fascinating connection has been revealed between the way two distinct Bose-Einstein condensates mix – transitioning from an immiscible, separated state to a miscible, blended one – and the surprising appearance of eight-fold rotational symmetry within the resulting density clusters. This isn’t simply a change in mixture; as the system moves towards miscibility, the density peaks don’t arrange themselves in the expected circular or square patterns. Instead, they spontaneously organize into structures exhibiting eight-fold symmetry – akin to a snowflake or an octagon – a phenomenon rooted in the underlying quantum mechanics and intercomponent interactions. This emergent order suggests that the phase transition isn’t merely a change in state, but a restructuring of the system at a fundamental level, resulting in a visually striking and theoretically important display of symmetry breaking and reformation.

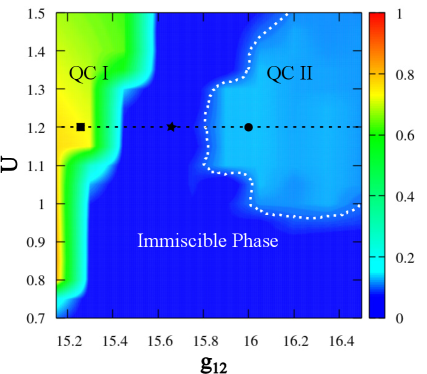
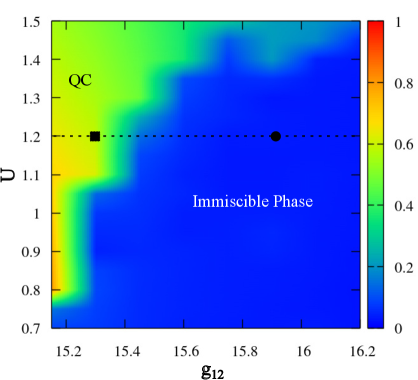
Researchers demonstrate precise control over the phase behavior of a binary Bose-Einstein condensate (BEC) through the application of carefully tuned two-dimensional, component-dependent periodic potentials and spin-dependent potentials. This manipulation allows for the sculpting of the condensate’s density distribution and the emergence of unique quantum states. Notably, key results, including significant shifts in phase transitions and the appearance of novel symmetries, are consistently observed when the intercomponent interaction strength, denoted as $g_{12}$ , reaches a value of 16.5. This specific interaction strength appears to act as a critical parameter, maximizing the influence of the applied potentials and providing a stable platform for observing emergent phenomena within the dual-species condensate system.

An imbalanced two-component Bose-Einstein condensate initialized with random fluctuations in a spin-dependent periodic lattice evolves to exhibit component separation, with the minority component's dynamics governed by an interaction strength of <span class="katex-eq" data-katex-display="false">g_{12} = 15.15</span>. — An imbalanced two-component Bose-Einstein condensate initialized with random fluctuations in a spin-dependent periodic lattice evolves to exhibit component separation, with the minority component’s dynamics governed by an interaction strength of $g_{12} = 15.15$ .

Towards Designed Aperiodicity: The Future of Quasicrystalline Materials

Characterizing the delicate balance between order and disorder in quasicrystalline materials requires precise quantitative tools, and the overlap parameter, when used in conjunction with the phase diagram, offers just that. This parameter essentially measures the degree of coherence between the periodic and aperiodic components within the system. A value of 1 signifies complete overlap and a fully ordered quasicrystal, while a decreasing value indicates a transition towards more disordered phases. Crucially, a parameter value reaching 0 denotes complete phase separation – a state where the periodic and aperiodic structures no longer coexist, and the unique properties of the quasicrystal are lost. This metric allows researchers to not only identify different phases but also to predict and control the conditions necessary to stabilize these exotic states of matter, paving the way for the design of tailored materials with unprecedented functionalities.

Researchers are increasingly turning to eightfold rotationally symmetric optical lattices as a means of fabricating and manipulating quasicrystalline states of matter. These lattices, created using interfering laser beams, provide a highly controlled environment for trapping and arranging atoms, effectively mimicking the long-range order found in true quasicrystals without the need for traditional materials synthesis. By precisely tuning the laser parameters – intensity, frequency, and polarization – scientists can engineer the lattice geometry to promote the emergence of these exotic phases. This approach offers significant advantages over conventional methods, enabling the study of quasicrystalline behavior in a variety of systems, from ultracold atoms to photonic structures, and opening doors to the potential development of materials with unique and previously unattainable properties. The ability to precisely control the atomic arrangement within these lattices promises a new era in the design and realization of novel quantum materials.

The emergence of a superfluid-quasicrystal state signifies a fundamentally new phase of matter, challenging conventional understandings of order and fluidity. This exotic state, neither perfectly crystalline nor entirely disordered, exhibits long-range aperiodic order alongside the ability of matter to flow without resistance – a combination previously thought impossible. Theoretical investigations suggest this phase arises from intricate interactions within many-body quantum systems, potentially realized in carefully engineered materials like ultracold atomic gases or specifically designed solid-state structures. Beyond the theoretical intrigue, the superfluid-quasicrystal state holds the promise of revolutionary applications in materials science, ranging from the development of novel energy-efficient technologies to the creation of ultra-sensitive sensors and potentially even quantum computing platforms. The unique combination of order and dissipationless flow offers pathways to manipulate matter at the quantum level with unprecedented precision, paving the way for materials with properties currently confined to the realm of speculation.

The phase diagram reveals that the imbalanced binary Bose-Einstein condensate exhibits quasicrystalline order in the coexistence phase <span class="katex-eq" data-katex-display="false">\mathcal{O}</span> (marked by the black square) and complete immiscibility (marked by the black circle) depending on the parameters <span class="katex-eq" data-katex-display="false">g_{12}</span> and <span class="katex-eq" data-katex-display="false">U</span>. — The phase diagram reveals that the imbalanced binary Bose-Einstein condensate exhibits quasicrystalline order in the coexistence phase $\mathcal{O}$ (marked by the black square) and complete immiscibility (marked by the black circle) depending on the parameters $g_{12}$ and $U$ .

The pursuit of order within chaos finds a curious echo in this work with Bose-Einstein condensates. The spontaneous emergence of aperiodicity-structures defying simple repetition-from seemingly ordered potentials is less a discovery of new physics, and more a forceful reminder that control is an illusion. It’s akin to attempting to dictate the pattern of smoke; one can influence the conditions, yet the final form remains stubbornly, beautifully unpredictable. As Simone de Beauvoir observed, “One is not born, but rather becomes,” and these condensates, subjected to spin-dependent potentials, don’t simply respond – they become something unforeseen, a testament to the system’s intrinsic agency. The intercomponent interactions aren’t merely forces, but ingredients of destiny, nudging the condensate toward novel states beyond initial expectation.

Beyond the Lattice

The spontaneous emergence of aperiodicity in these binary condensates isn’t a revelation of order, but a reminder that ‘order’ is simply the lowest-energy configuration someone hasn’t bothered to disrupt yet. This work demonstrates a pathway – spin-dependent modulation – to nudge systems toward these quasicrystalline states, but the dependence on finely tuned intercomponent interactions feels… precarious. It’s a delicate balancing act, and the slightest deviation in parameters will likely send the condensate collapsing back into the comfortably predictable. The question isn’t whether such phases can exist, but how robust they are against the inevitable noise of any real experiment.

Future iterations will likely focus on expanding beyond the binary case. What happens when the system’s complexity increases? Does aperiodicity become more stable, or does it simply dissolve into featureless chaos? More intriguingly, can these systems be used as analog quantum simulators for genuinely aperiodic physical systems – materials where the very structure defies simple repetition? That’s a tempting thought, though simulating a system one barely understands with another one that’s equally opaque feels… recursive.

Ultimately, this research highlights a persistent truth: data isn’t about finding answers, it’s about refining the questions. The observed phases aren’t ‘there’ to be discovered, they’re consequences of the experiment. And the experiment, as always, is just a controlled way to irritate the universe until it tells you something interesting.

Original article: https://arxiv.org/pdf/2602.13129.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/