Twisted Skies: Unveiling Magnetic Textures in Moiré Materials

Author: Denis Avetisyan

A new theoretical framework explains the emergence of skyrmion crystals and complex magnetic behavior in layered materials with precisely controlled twist angles.

The study of skyrmion-crystal magnetophonon dispersion reveals a transition in frequency scaling from <span class="katex-eq" data-katex-display="false"> \omega \sim q^2 </span> for short-range elasticity to <span class="katex-eq" data-katex-display="false"> \omega \sim q^{3/2} </span> with long-range Coulomb interactions, further complicated by the emergence of a pinning-induced gap under weak moiré pinning. — The study of skyrmion-crystal magnetophonon dispersion reveals a transition in frequency scaling from $\omega \sim q^2$ for short-range elasticity to $\omega \sim q^{3/2}$ with long-range Coulomb interactions, further complicated by the emergence of a pinning-induced gap under weak moiré pinning.

This work develops a 1/J expansion to reveal emergent gauge fields and a non-adiabatic magneto-elastic theory for skyrmion-crystal phases in moiré quantum materials.

The emergence of correlated electronic states in moiré quantum materials presents a challenge to conventional band structure paradigms. This is addressed in ‘Controlled Theory of Skyrmion Chern Bands in Moiré Quantum Materials: Quantum Geometry and Collective Dynamics’, which develops a systematic analytical framework-based on a $\frac{1}{J}$ expansion-to describe these systems. Our approach reveals emergent non-Abelian gauge structures and a skyrmion-crystal magneto-elastic effective theory extending beyond adiabatic approximations, predicting novel signatures from Umklapp scattering to noncommutative phonons. Can these analytically derived features be leveraged to fully understand and predict the exotic behavior observed in twisted heterostructures like transition-metal dichalcogenides and graphene on hexagonal boron nitride?

The Limits of Conventional Approximation

Condensed matter physics traditionally streamlines calculations by employing the adiabatic approximation – a concept positing that systems evolve slowly enough to remain in their ground state throughout a process. This simplification allows physicists to model complex materials with relative ease, but it inherently assumes a disconnect between electronic and atomic motions. However, this assumption isn’t universally valid; when atomic changes occur rapidly relative to the electrons, the system is driven away from its instantaneous ground state, and the adiabatic approximation falters. Consequently, crucial physical phenomena – such as non-equilibrium dynamics and the emergence of exotic quantum states – can be obscured or misinterpreted when relying solely on this conventional approach. Recognizing the limitations of adiabaticity is therefore essential for accurately describing materials where strong electron correlations and rapid atomic changes are present, paving the way for a more complete understanding of their behavior.

The adiabatic approximation, a cornerstone of conventional condensed matter physics, falters when applied to strongly correlated moiré materials. These engineered van der Waals heterostructures exhibit strong interactions between electrons, leading to scenarios where the system cannot respond instantaneously to external changes – a key assumption of adiabaticity. Consequently, traditional perturbative methods and band structure calculations based on this approximation yield inaccurate predictions of their observed phenomena, such as correlated insulating states and unconventional superconductivity. Researchers are therefore developing novel theoretical frameworks – including non-adiabatic quantum dynamics, many-body localization theory, and diagrammatic techniques beyond mean-field approximations – to capture the complex interplay of electron correlations and lattice interactions in these materials. These advanced tools aim to provide a more complete and accurate description of the exotic quantum states and emergent behaviors found within strongly correlated moiré systems, paving the way for the design of novel quantum devices.

The continued advancement of quantum technologies hinges on a thorough understanding of when established theoretical frameworks falter. The adiabatic approximation, a cornerstone of condensed matter physics, assumes systems evolve slowly enough to remain in their ground state; however, in strongly correlated moiré materials-where electron interactions are dominant-this assumption frequently fails. Recognizing these limitations isn’t merely an academic exercise; it’s a prerequisite for accurately predicting and ultimately harnessing the exotic properties emerging in these materials. Without accounting for the non-adiabatic effects-the transitions between quantum states induced by rapid changes-researchers risk misinterpreting experimental results and overlooking potential applications in areas like superconductivity and quantum computation. Therefore, developing and implementing theoretical tools that go beyond the adiabatic limit represents a critical frontier in materials science, paving the way for the realization of novel quantum devices and a deeper understanding of emergent phenomena.

A moiré unit cell exhibiting a skyrmion-like pseudospin texture allows for controlled decomposition of emergent flux density <span class="katex-eq" data-katex-display="false"> \bm{b}(\bm{r}) = \bm{b}_{0} + \delta \bm{b}(\bm{r}) </span> via local <span class="katex-eq" data-katex-display="false"> SU(2) </span> rotations, a Schrieffer-Wolff expansion, and ultimately a simplified single-branch Landau-level description modulated by average flux <span class="katex-eq" data-katex-display="false"> \bm{b}_{0} </span>. — A moiré unit cell exhibiting a skyrmion-like pseudospin texture allows for controlled decomposition of emergent flux density $\bm{b}(\bm{r}) = \bm{b}_{0} + \delta \bm{b}(\bm{r})$ via local $SU(2)$ rotations, a Schrieffer-Wolff expansion, and ultimately a simplified single-branch Landau-level description modulated by average flux $\bm{b}_{0}$ .

A Systematic Expansion for Correlated Systems

The 1/J expansion is a systematic technique employed to investigate strongly correlated systems, particularly those found in moiré materials. This method frames the analysis as an operator expansion in powers of the inverse of the interaction energy scale, $J^{-1}$ . Unlike traditional perturbation theories which can fail when interactions are strong, the 1/J expansion directly addresses non-perturbative effects by expressing physical observables as a series of operators. Each term in the expansion corresponds to a specific order in $J^{-1}$ , allowing for a controlled approximation where higher-order terms systematically refine the results and capture increasingly complex many-body effects. This approach facilitates the calculation of physical properties by mapping the original strongly interacting problem onto a series of simpler, solvable problems.

Traditional perturbation theory relies on a weak coupling limit to approximate system behavior, becoming inaccurate when interactions are strong. The 1/J expansion circumvents this limitation by formulating a systematic expansion in powers of 1/J, where J represents the characteristic interaction strength. This approach doesn’t treat interactions as a small perturbation; instead, it directly incorporates strong correlations into the formalism. Consequently, the 1/J expansion effectively addresses non-adiabatic effects – those arising from the inability of the system to instantaneously adjust to changes in its environment – which become prominent in strongly interacting systems where standard perturbative methods fail. This allows for the calculation of physical observables even when interactions dominate the kinetic energy, providing a more accurate description of correlated phenomena.

The 1/J expansion facilitates a controlled approach to modeling strongly correlated systems by enabling the inclusion of higher-order terms in the operator expansion. Each successive order in the expansion, represented by increasing powers of $1/J$ where J is the interaction strength, incorporates additional interaction effects and many-body correlations. This systematic refinement allows for the calculation of physical observables with increasing accuracy, moving beyond the limitations of perturbative approaches that typically truncate the expansion at low orders. Consequently, higher-order terms capture increasingly complex physics, such as many-body resonances and non-perturbative effects, leading to predictions that more closely align with experimental observations or more accurate numerical simulations.

Emergent Gauge Structures and Unconventional Responses

The application of a 1/J expansion – where J represents the strength of the interlayer hopping – to moiré materials reveals the emergence of U(1) gauge fields. This arises from the strong correlations induced by the geometric frustration inherent in the moiré lattice and the associated flat bands near the Fermi level. Specifically, the kinetic energy of the electrons, when expanded in powers of 1/J, generates terms that can be interpreted as interactions with these emergent gauge fields. These fields are not fundamental but rather collective modes arising from the interplay between electron-electron interactions and the unique geometric constraints imposed by the moiré superlattice, effectively modifying the system’s low-energy physics and leading to novel electronic properties.

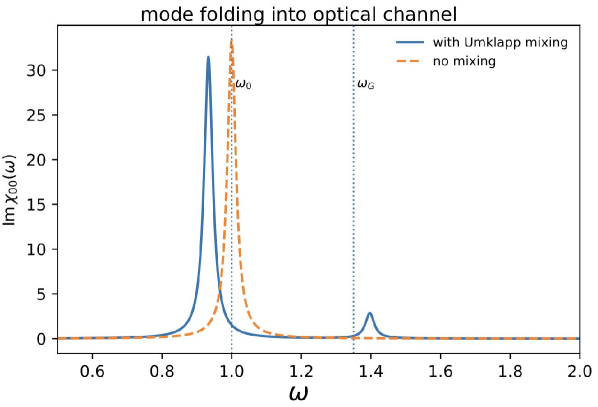
The emergence of gauge fields within moiré materials, intrinsically linked to the system’s quantum geometry – specifically, the band structure and associated Berry curvature – results in unconventional electronic responses. Our analysis demonstrates the manifestation of the Umklapp response, a phenomenon where electron scattering is enhanced at reciprocal lattice vectors $\pm \frac{2\pi}{a}$ , due to the altered momentum space topology. This response deviates from conventional behavior predicated on a simple free electron model and arises from the coupling between the electrons and the emergent gauge potential, fundamentally modifying the system’s transport properties and observed band structure.

Analysis of moiré material lattice dynamics reveals evidence of noncommutative phonons, indicating a departure from the standard harmonic oscillator model used to describe lattice vibrations. This noncommutativity arises from the material’s specific kinematic properties, where the spatial coordinates associated with atomic displacements do not commute-that is, $[x_i, x_j] \neq 0$ -leading to a modification of the phonon dispersion relation. Consequently, the classical description of phonons as plane waves breaks down, necessitating a quantum mechanical treatment to accurately model the lattice vibrational behavior and predict material properties dependent on these modes.

Umklapp mixing between <span class="katex-eq" data-katex-display="false">m{G}=0</span> and <span class="katex-eq" data-katex-display="false">m{G}\neq 0</span> density sectors transfers spectral weight, enabling optical activity of collective modes in the <span class="katex-eq" data-katex-display="false">m{G}=0</span> channel through a process known as mode folding. — Umklapp mixing between $m{G}=0$ and $m{G}\neq 0$ density sectors transfers spectral weight, enabling optical activity of collective modes in the $m{G}=0$ channel through a process known as mode folding.

Moiré Heterostructures: A Playground for Exotic Quantum Phenomena

Investigations into moiré heterostructures reveal a surprising simplicity in their complex behavior: the system’s fundamental properties are accurately described by a single-particle Hamiltonian. This mathematical framework, incorporating the effects of spin-orbit coupling – an interaction between an electron’s spin and its motion – allows for a streamlined understanding of these layered materials. Effectively, the intricate many-body interactions within the heterostructure can be mapped onto the behavior of a single, albeit complex, particle. This reduction in complexity doesn’t sacrifice accuracy, providing a powerful tool for predicting and interpreting the exotic quantum phenomena observed in these systems, and opening avenues for designing novel electronic devices based on their unique properties. The $H = \frac{p^2}{2m} + V(r) + \alpha \vec{L} \cdot \vec{\sigma}$ Hamiltonian effectively captures the essential physics at play.

Analyzing complex quantum systems often requires navigating extraordinarily high-dimensional spaces, making calculations computationally expensive and conceptually challenging. Researchers have successfully employed a projection method to dramatically simplify the analysis of moiré heterostructures by focusing specifically on the system’s low-energy behavior. This technique effectively isolates the most relevant degrees of freedom – those governing the phenomena observed at low energies – while discarding the influence of higher-energy, less impactful states. The result is a significantly reduced Hamiltonian, allowing for accurate predictions of the system’s properties without sacrificing crucial details; this streamlined approach enables a more tractable and insightful investigation into the exotic quantum phenomena arising within these uniquely layered materials.

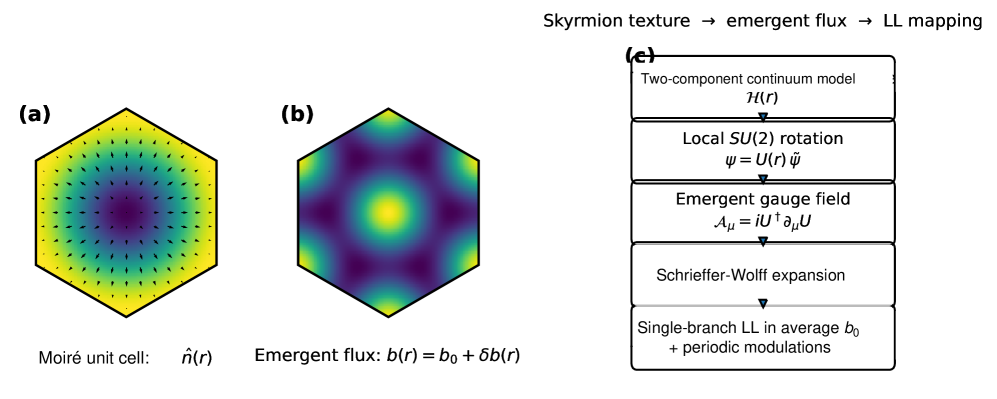
Moiré heterostructures exhibit a surprising connection between their inherent translational symmetries and magnetic behavior, resulting in the formation of a novel mathematical construct known as a magnetic-translation group. This group extends traditional translation algebra by incorporating the magnetic properties of the material, effectively treating magnetic translations as fundamental symmetry operations alongside spatial translations. The consequence is a richer symmetry description than typically observed, where the interplay between these operations dictates the allowed quantum states and low-energy excitations within the heterostructure. This unique symmetry framework not only provides a deeper understanding of the material’s quantum properties but also opens possibilities for designing novel electronic devices leveraging these emergent symmetries to control electron behavior – effectively manipulating charge through the interplay of space and magnetism at the nanoscale.

The real-space texture of skyrmions reveals a relationship between emergent flux <span class="katex-eq" data-katex-display="false">b(\bm{r})</span>, derived from the pseudospin texture <span class="katex-eq" data-katex-display="false">\hat{\bm{n}}(\bm{r})</span>, and the pointwise two-level inequality relating the trace of the quantum metric <span class="katex-eq" data-katex-display="false">\mathrm{Tr}\,g(\bm{r})</span> to the magnitude of the flux, demonstrating a geometric origin for flux inhomogeneity. — The real-space texture of skyrmions reveals a relationship between emergent flux $b(\bm{r})$ , derived from the pseudospin texture $\hat{\bm{n}}(\bm{r})$ , and the pointwise two-level inequality relating the trace of the quantum metric $\mathrm{Tr}\,g(\bm{r})$ to the magnitude of the flux, demonstrating a geometric origin for flux inhomogeneity.

Future Directions: Skyrmion Crystals and Beyond

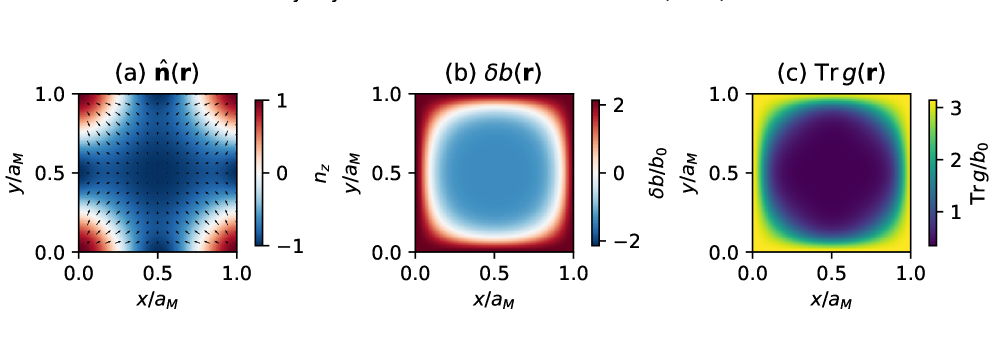
Recent investigations have established a theoretical framework – the Skyrmion-Crystal Effective Theory – for interpreting the intricate magneto-elastic behavior exhibited by skyrmion crystals within moiré materials. These crystals, nanoscale arrangements of magnetic textures, respond to external stimuli in ways dictated by the interplay between magnetic interactions and the underlying material’s elasticity. This work provides a crucial foundation for accurately modeling these responses, accounting for how the crystal lattice deforms under magnetic forces and, conversely, how applied stress alters the magnetic configuration. By detailing this relationship, researchers gain a powerful tool to predict and control the properties of these systems, opening avenues for exploiting their unique characteristics in future technological applications. Understanding this magneto-elastic coupling is therefore paramount to harnessing the full potential of skyrmion crystals and moiré materials for advanced devices.

The predictive power of the Skyrmion-Crystal Effective Theory extends beyond its initial formulation through a systematic refinement process involving higher-order terms in the 1/J expansion. This methodology allows researchers to move past approximations and delve into increasingly intricate magneto-elastic behaviors within moiré materials. By meticulously incorporating these terms – representing smaller, yet significant, contributions to the overall energy – the theory can account for subtle distortions, interactions, and emergent phenomena not captured in simpler models. Consequently, predictions regarding skyrmion crystal stability, dynamics, and response to external stimuli become more accurate and nuanced, offering a pathway to understanding – and ultimately harnessing – the full range of possibilities offered by these unique quantum systems. This iterative refinement isn’t merely about improving precision; it opens doors to discovering entirely new behaviors and functionalities within moiré materials, potentially unlocking innovations in quantum information processing and advanced materials science.

The refined understanding of skyrmion crystals within moiré materials offers a pathway towards constructing innovative quantum devices. These materials, with their precisely engineered periodic structures, allow for the tailoring of magnetic interactions and the creation of stable, controllable skyrmionic states – potential carriers of quantum information. Exploiting these properties could lead to the development of robust and energy-efficient spintronic devices, and even entirely new paradigms for quantum computation and communication. Further exploration promises to unlock the full potential of moiré materials, not just as platforms for fundamental physics research, but as key components in the next generation of quantum technologies, pushing the boundaries of information processing and materials science.

The pursuit of a controlled theory, as demonstrated in this exploration of moiré materials, echoes a fundamental principle of mathematical elegance. This work meticulously dissects the interplay between quantum geometry and collective dynamics, striving for a provable understanding beyond empirical observation. It is a demonstration of how a systematic expansion – the 1/J expansion, in this case – can reveal underlying structures and emergent phenomena. As Epicurus observed, “It is not the pursuit of pleasure itself, but the removal of pain that provides happiness.” Similarly, this research doesn’t merely observe complex behavior in moiré materials; it seeks to remove the ‘pain’ of uncertainty by establishing a rigorous, mathematically grounded framework, particularly in its treatment of non-adiabaticity and Umklapp scattering.

Future Directions

The presented framework, while establishing a rigorous foundation for understanding emergent phenomena in moiré materials via a 1/J expansion, does not resolve the inherent difficulty in connecting microscopic parameters to macroscopic observables. The adiabatic limit, so often invoked, proves insufficient; however, the inclusion of non-adiabatic effects, while necessary, introduces complexities demanding further scrutiny. The precise characterization of the noncommutative phonon modes, and their contribution to Umklapp scattering processes, remains an open question. A complete analytical treatment of these interactions requires a formalism that transcends perturbation theory – a challenge that may necessitate the exploration of alternative mathematical structures.

The resulting magneto-elastic effective theory for the skyrmion-crystal phase, though elegantly derived, relies on assumptions regarding the long-wavelength behavior of the underlying lattice. The validity of these assumptions in the presence of strong correlations, or near phase transitions, warrants careful investigation. Future work should focus on developing a systematic approach to account for short-wavelength fluctuations and their influence on the stability and dynamics of the skyrmion lattice. The ultimate test lies in predicting experimental signatures that unambiguously confirm the existence of the predicted emergent gauge fields and their role in mediating interactions between skyrmions.

It is, perhaps, ironic that a pursuit of analytical control – a desire for provable correctness – inevitably leads to the identification of further, more subtle, sources of approximation. The field demands not merely computational efficiency, but a relentless pursuit of mathematical elegance, a willingness to confront the limits of perturbative approaches, and a recognition that true understanding lies not in fitting parameters, but in revealing the underlying geometrical and topological invariants that govern these remarkable materials.

Original article: https://arxiv.org/pdf/2602.15016.pdf

Contact the author: https://www.linkedin.com/in/avetisyan/